
分析 由条件利用二倍角的正切公式求得tanθ的值,再利用诱导公式、同角三角函数的基本关系求得要求式子的值.
解答 解:角θ的终边在第三象限,tan2θ=-2$\sqrt{2}$=$\frac{2tanθ}{1{-tan}^{2}θ}$,∴tanθ=$\sqrt{2}$,或 tanθ=-$\frac{\sqrt{2}}{2}$(舍去)
则sin2θ+sin(3π-θ)cos(2π+θ)-$\sqrt{2}$cos2θ=sin2θ+sinθcosθ-$\sqrt{2}$cos2θ
=$\frac{{sin}^{2}θ+sinθcosθ-\sqrt{2}{•cos}^{2}θ}{{sin}^{2}θ{+cos}^{2}θ}$=$\frac{{tan}^{2}θ+tanθ-\sqrt{2}}{{tan}^{2}θ+1}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查二倍角的正切公式,诱导公式、同角三角函数的基本关系,属于基础题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 20.7% | B. | 29.3% | C. | 58.6% | D. | 41.4% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
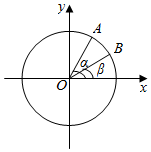 如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
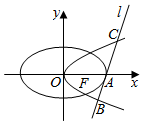 如图,抛物线C:y2=8x的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,离心率为$\frac{1}{2}$,且F为线段OA的中点,O为坐标原点.
如图,抛物线C:y2=8x的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,离心率为$\frac{1}{2}$,且F为线段OA的中点,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(万元) | 2 | 4 | 5 | 6 | 8 |
| y(万元) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com