
分析 求得两圆的圆心和半径,设双曲线x2-$\frac{{y}^{2}}{15}$=1的左右焦点为F1(-4,0),F2(4,0),连接PF1,PF2,F1M,F2N,运用勾股定理和双曲线的定义,结合三点共线时,距离之和取得最小值,计算即可得到所求值.
解答 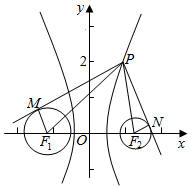 解:圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
解:圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
圆C2:(x-4)2+y2=1的圆心为(4,0),半径为r2=1,
设双曲线x2-$\frac{{y}^{2}}{15}$=1的左右焦点为F1(-4,0),F2(4,0),
连接PF1,PF2,F1M,F2N,可得
|PM|2-|PN|2=(|PF1|2-r12)-(|PF2|2-r22)
=(|PF1|2-4)-(|PF2|2-1)
═|PF1|2-|PF2|2-3=(|PF1|-|PF2|)(|PF1|+|PF2|)-3
=2a(|PF1|+|PF2|-3=2(|PF1|+|PF2|)-3≥2•2c-3=2•8-3=13.
当且仅当P为右顶点时,取得等号,即最小值13.
故答案为:13.
点评 本题考查最值的求法,注意运用双曲线的定义和圆的方程,考查三点共线的性质,以及运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1-ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{10},0}),({-\sqrt{10},0})$ | B. | $({0,\sqrt{10}}),({0,-\sqrt{10}})$ | C. | (0,3),(0,-3) | D. | (3,0),(-3,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k1+k3=k2 | B. | k1+k3=2k2 | C. | k1k3=k2 | D. | k1k3=k${\;}_{2}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 | ||
| C. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1和$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1或$\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
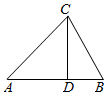 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com