
| A. | k1+k3=k2 | B. | k1+k3=2k2 | C. | k1k3=k2 | D. | k1k3=k${\;}_{2}^{2}$ |
分析 求得双曲线的右焦点,设直线1的方程为x=my+5,代入双曲线的方程16x2-9y2=144,运用韦达定理,设M($\frac{9}{5}$,t),运用直线的斜率公式可得k2=$\frac{t}{\frac{9}{5}-5}$=-$\frac{5t}{16}$,k1+k3=$\frac{{y}_{1}-t}{{x}_{1}-\frac{9}{5}}$+$\frac{{y}_{2}-t}{{x}_{2}-\frac{9}{5}}$,代入韦达定理,化简整理即可得到k1+k3=2k2.
解答 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1右焦点F为(5,0),
设直线1的方程为x=my+5,
代入双曲线的方程16x2-9y2=144,可得
(16m2-9)y2+160my+256=0,
设A(x1,y1),B(x2,y2),
即有y1+y2=-$\frac{160m}{16{m}^{2}-9}$,y1y2=$\frac{256}{16{m}^{2}-9}$,
设M($\frac{9}{5}$,t),可得k2=$\frac{t}{\frac{9}{5}-5}$=-$\frac{5t}{16}$,
k1+k3=$\frac{{y}_{1}-t}{{x}_{1}-\frac{9}{5}}$+$\frac{{y}_{2}-t}{{x}_{2}-\frac{9}{5}}$=$\frac{{y}_{1}-t}{m{y}_{1}+\frac{16}{5}}$+$\frac{{y}_{2}-t}{m{y}_{2}+\frac{16}{5}}$
=$\frac{2m{y}_{1}{y}_{2}+(\frac{16}{5}-mt)({y}_{1}+{y}_{2})-\frac{32}{5}t}{{m}^{2}{y}_{1}{y}_{2}+\frac{16}{5}m({y}_{1}+{y}_{2})+\frac{256}{25}}$,
代入韦达定理,可得k1+k3=$\frac{2m•256+(\frac{16}{5}-mt)•(-160m)-\frac{32}{5}t(16{m}^{2}-9)}{256{m}^{2}-2•256{m}^{2}+\frac{256}{25}(16{m}^{2}-9)}$=-$\frac{5t}{8}$,
即有k1+k3=2k2.
故选:B.
点评 本题考查双曲线的方程和性质,注意运用直线方程和双曲线的方程联立,运用韦达定理,考查直线的斜率公式的运用,考查化简整理的运算能力,属于中档题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
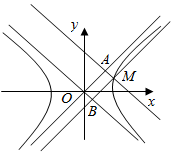 如图,设M为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上任意一点,O为原点,过点M作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,探求平行四边形MAOB的面积,由此可以发现什么结论?
如图,设M为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上任意一点,O为原点,过点M作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,探求平行四边形MAOB的面积,由此可以发现什么结论?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com