
分析 可设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CA}$=$\overrightarrow{c}$,由题意可得cosB=-$\frac{1}{5}$,sinB=$\frac{2\sqrt{6}}{5}$,cosC=$\frac{1}{3}$,sinC=$\frac{2\sqrt{2}}{3}$,由两角和的正弦公式和余弦公式,可得sinA,cosA,再由正弦定理和向量的数量积的定义,计算即可得到所求值.
解答  解:可设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CA}$=$\overrightarrow{c}$,
解:可设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CA}$=$\overrightarrow{c}$,
$\overrightarrow{a}$与$\overrightarrow{b}$的夹角余弦为$\frac{1}{5}$,可得cosB=-$\frac{1}{5}$,sinB=$\frac{2\sqrt{6}}{5}$,
$\overrightarrow{b}$与$\overrightarrow{c}$的夹角余弦为为-$\frac{1}{3}$,可得cosC=$\frac{1}{3}$,sinC=$\frac{2\sqrt{2}}{3}$,
即有sinA=sin(B+C)=sinBcosC+cosBsinC
=$\frac{2\sqrt{6}}{5}$×$\frac{1}{3}$+(-$\frac{1}{5}$)×$\frac{2\sqrt{2}}{3}$=$\frac{2\sqrt{6}-2\sqrt{2}}{15}$,
cosA=-cos(B+C)=-cosBcosC+sinBsinC
=$\frac{1}{5}$×$\frac{1}{3}$+$\frac{2\sqrt{6}}{5}$×$\frac{2\sqrt{2}}{3}$=$\frac{1+8\sqrt{3}}{15}$,
由正弦定理可得$\frac{|\overrightarrow{a}|}{sinC}$=$\frac{|\overrightarrow{b}|}{sinA}$=$\frac{|\overrightarrow{c}|}{sinB}$=$\frac{1}{\frac{2\sqrt{6}-2\sqrt{2}}{15}}$,
可得|$\overrightarrow{a}$|=$\frac{15}{2\sqrt{6}-2\sqrt{2}}$×$\frac{2\sqrt{2}}{3}$=$\frac{5}{2}$(1+$\sqrt{3}$),
|$\overrightarrow{c}$|=$\frac{15}{2\sqrt{6}-2\sqrt{2}}$×$\frac{2\sqrt{6}}{5}$=$\frac{1}{2}$(9+3$\sqrt{3}$),
即有$\overrightarrow{a}$•$\overrightarrow{c}$=|$\overrightarrow{a}$|•|$\overrightarrow{c}$|•cosA=$\frac{5}{2}$(1+$\sqrt{3}$)×$\frac{1}{2}$(9+3$\sqrt{3}$)×$\frac{1+8\sqrt{3}}{15}$
=$\frac{26\sqrt{3}+51}{2}$.
故答案为:$\frac{26\sqrt{3}+51}{2}$.
点评 本题考查向量的数量积的定义,考查正弦定理的运用,以及三角函数的求值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | k1+k3=k2 | B. | k1+k3=2k2 | C. | k1k3=k2 | D. | k1k3=k${\;}_{2}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{11}{6}$] | B. | [$\frac{1}{2}$,$\frac{11}{6}$) | C. | ($\frac{1}{3}$,$\frac{13}{6}$] | D. | [$\frac{1}{3}$,$\frac{13}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
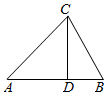 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com