
(本小题满分12分)设函数f(x)=m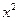 -mx-1.
-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;
(2)对于x∈[1,3],f(x)<0恒成立,求m的取值范围.
科目:高中数学 来源: 题型:解答题
设 ,
,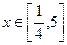 , 其中
, 其中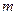 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出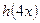 的定义域(2分);
的定义域(2分);
(文)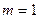 时,直接写出
时,直接写出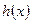 的值域(4分)
的值域(4分)
(2)、(文、理)求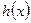 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数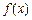
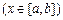 ,定义:
,定义: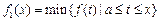
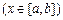 ,
,
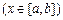 .其中,
.其中, 表示函数
表示函数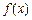 在
在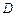 上的最小值,
上的最小值,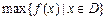 表示函数
表示函数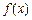 在
在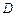
 上的最大值.例如:
上的最大值.例如: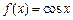 ,
,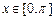 ,则
,则 ,
,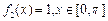 ,
,
(理)当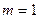 时,设
时,设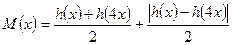 ,不等式
,不等式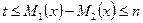
恒成立,求 的取值范围(11分);
的取值范围(11分);
(文)当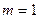 时,
时,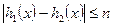 恒成立,求
恒成立,求 的取值范围(8分);
的取值范围(8分);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数 ,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知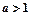 ,函数
,函数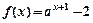
(1)求 的反函数
的反函数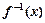 ;
;
(2)若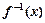 在[0,1]上的最大值与最小值互为相反数,求
在[0,1]上的最大值与最小值互为相反数,求 ;
;
(3)若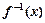 的图像不经过第二象限,求
的图像不经过第二象限,求 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数
 ,其图象过点(
,其图象过点( ,
, ).
).
(1)求 的值及
的值及 最小正周期;
最小正周期;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数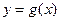 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com