练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知（1+x）（1-2x）6=a0+a1（x-1）+a2（x-1）2+…+a7（x-1）7，则a3=（　　）
    A．220B．350C．380D．410

    分析 由（1+x）（1-2x）6=[（x-1）+2][2（x-1）+1]6，可得[（x-1）+2][2（x-1）+1]6　=a0+a1（x-1）+a2（x-1）2+…+a7（x-1）7，求得a3的值．

    解答 解：由（1+x）（1-2x）6=[（x-1）+2][2（x-1）+1]6，
    （1+x）（1-2x）6=a0+a1（x-1）+a2（x-1）2+…+a7（x-1）7，
    ∴[（x-1）+2][2（x-1）+1]6　=a0+a1（x-1）+a2（x-1）2+…+a7（x-1）7，
    ∴a3=C6222+2C6323=60+320=380，
    故选：C．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．为建设美丽乡村，政府欲将一块长12百米，宽5百米的矩形空地ABCD建成生态休闲园，园区内有一景观湖EFG（图中阴影部分），以AB所在直线为x轴，AB的垂直平分线为y轴，建立平面直角坐标系xOy（如图所示）．景观湖的边界线符合函数y=x+$\frac{1}{x}$（x＞0）模型，园区服务中心P在x轴正半轴上，PO=$\frac{4}{3}$百米．
    （1）若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM，求OM的最短长度；
    （2）若在线段DE上设置一园区出口Q，试确定Q的位置，使通道PQ最短．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．过点M（m，0）（m＞0）作直线l，与抛物线y2=4x有两交点A，B，F是抛物线的焦点，若$\overrightarrow{FA}•\overrightarrow{FB}＜0$，则m的取值范围是（3-2$\sqrt{2}$，3+2$\sqrt{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某校举办“中国诗词大赛”活动，某班派出甲乙两名选手同时参加比赛．大赛设有15个诗词填空题，其中“唐诗”、“宋词”和“毛泽东诗词”各5个．每位选手从三类诗词中各任选1个进行作答，3个全答对选手得3分，答对2个选手得2分，答对1个选手得1分，一个都没答对选手得0分．已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5，4，3，乙能答对的题目个数依此为4，5，4，假设每人各题答对与否互不影响，甲乙两人答对与否也互不影响．
    求：
    （Ⅰ）甲乙两人同时得到3分的概率；
    （Ⅱ）甲乙两人得分之和ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=$\sqrt{3}$sin2x+sinxcosx-$\frac{\sqrt{3}}{2}$
    （1）求函数y=f（x）在[0，$\frac{π}{2}$]上的单调递增区间；
    （2）将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位长度，再将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到函数y=g（x）的图象，求证：存在无穷多个互不相同的整数x0，使得g（x0）＞$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$右支上的一点，其左、右焦点分别为F1，F2，若△PF1F2的内切圆I与x轴相切于点A，过F2作PI的垂线，重足为B，O为坐标原点，那么$\frac{{|{OA}|}}{{|{OB}|}}$的值为（　　）
    A．1B．$\sqrt{2}$C．$\frac{b}{a}$D．$\frac{a}{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知函数$f（x）={2^x}+\frac{1}{{{2^{x+2}}}}$，则f（x）取最小值时对应的x的值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．圆（x-1）2+（y+1）2=10的半径为（　　）
    A．（1，-1）B．（-1，1）C．$\sqrt{10}$D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某多面体的三视图如下图所示（网格纸上小正方形的边长为1），则该多面体的表面积为（　　）
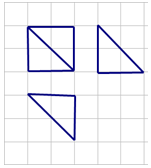
    A．$8+4\sqrt{2}$B．$6+4\sqrt{2}$C．12D．$8+5\sqrt{2}$

    查看答案和解析>>

    同步练习册答案