
分析 设出B,C坐标,代入椭圆方程,利用直线的斜率关系,转化求解椭圆的离心率即可.
解答 解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的上顶点为A(0,b),直线y=kx与椭圆交于B,C两点,
设B(m,n),则C(-m,-n),kAB•kAC=-$\frac{3}{4}$,$\frac{{m}^{2}}{{a}^{2}}+\frac{{n}^{2}}{{b}^{2}}=1$,n=km.n2=$\frac{{{b}^{2}a}^{2}-{{b}^{2}m}^{2}}{{a}^{2}}$,
可得:$\frac{n-b}{m}•\frac{-n-b}{-m}=-\frac{3}{4}$,
即:$\frac{{n}^{2}-{b}^{2}}{{m}^{2}}=-\frac{3}{4}$,
可得:$\frac{\frac{{b}^{2}{a}^{2}-{b}^{2}{m}^{2}}{{a}^{2}}-{b}^{2}}{{m}^{2}}$=$-\frac{3}{4}$,
可得:$-\frac{{b}^{2}}{{a}^{2}}=-\frac{3}{4}$,即$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{4}$,
解得e=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆的简单性质的应用,直线的斜率的求法,注意直线以及椭圆的对称性是解题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
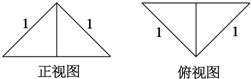 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com