
����Ŀ��Ϊ����ij����Ⱥ�������Ѫѹ�Ĺ�ϵ���ü�������������Ӹõ���������20��60�����Ⱥ�г�ȡ200�˲���Ѫѹ��������£�
��Ѫѹ | �Ǹ�Ѫѹ | �ܼ� | |
����20��39�� | 12 |
| 100 |
����40��60�� |
| 52 | 100 |
�ܼ� | 60 |
| 200 |
(1)������е�![]() ��
��![]() ��
��![]() ֵ���Ƿ���99%�İ�����Ϊ��Ѫѹ�������йأ���˵�����ɣ�
ֵ���Ƿ���99%�İ�����Ϊ��Ѫѹ�������йأ���˵�����ɣ�
(2)�ִ���60����Ѫѹ�����а�������÷ֲ�����ķ�����ȡ5�ˣ��ٴ���5���������ȡ2�ˣ���ǡ��һ������������20��39��ĸ���.
���ο���ʽ���ο����ݣ� ![]() =
=![]()
P(k2��k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡���1����99.9%�İ�����2��![]()
����������������������������������������������б������ݽ���������⣻�����������������������оٷ����ŵ���ͼ��㹫ʽ��⣺
(1)��![]() ��
�� ![]() �����
�����![]() =88��
=88�� ![]() =48��
=48�� ![]() =52+
=52+ ![]() =140��
=140��
��![]() =
=![]() ��30.857��
��30.857��
����30.857��10.828��������99.9%�İ�����Ϊ����Ѫѹ�������й�����
��2���ɷֲ��������֪��������20��39�Ļ����г�ȡ������Ϊ1������˼�Ϊ![]() ��������40��60�Ļ����г�ȡ������Ϊ4����4�˷ֱ��Ϊ
��������40��60�Ļ����г�ȡ������Ϊ4����4�˷ֱ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����ȡ2����{
����ȡ2����{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� }��{
![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��10�ֲ�ͬ��ѡ��������ǡ��1��������20��39��Ѫѹ������{
}��10�ֲ�ͬ��ѡ��������ǡ��1��������20��39��Ѫѹ������{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��{
}��{![]() ��
�� ![]() }��4�֣�
}��4�֣�
��ѡȡ��������Ѫѹ������ǡ�к�1��������20��39�ĸ���Ϊ![]() =
=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��12�£����е��������п�����Ⱦָ������������������ȾΪ2015�����������ص���Ⱦ���̣�Ϊ��̽����������![]() ��Ũ���Ƿ���أ��ֲɼ�������ij����2015��12�·�ij��������һ��������ijһʱ��γ�������
��Ũ���Ƿ���أ��ֲɼ�������ij����2015��12�·�ij��������һ��������ijһʱ��γ�������![]() �����������
�����������
ʱ�� | ����һ | ���ڶ� | ������ | ������ | ������ | ������ | ������ |
������ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
��1����ɢ��ͼ֪![]() ��
��![]() ����������ع�ϵ����
����������ع�ϵ����![]() ����
����![]() �����Իع鷽�̣�����ʾ���ݣ�
�����Իع鷽�̣�����ʾ���ݣ� ![]() ��
��
��2����I�����ã�1������Ļع鷽�̣�Ԥ����г�����Ϊ12����ʱ![]() ��Ũ�ȣ���II���涨����һ����
��Ũ�ȣ���II���涨����һ����![]() ��Ũ��ƽ��ֵ��
��Ũ��ƽ��ֵ��![]() �ڣ����������ȼ�Ϊ�ţ���һ����
�ڣ����������ȼ�Ϊ�ţ���һ����![]() ��Ũ��ƽ��ֵ��
��Ũ��ƽ��ֵ��![]() �ڣ����������ȼ�Ϊ����Ϊʹ����ij�տ�������Ϊ�Ż���Ϊ������Ӧ���Ƶ��쳵�������������������������������Ϊ��λ�������������ο���ʽ���ع�ֱ�ߵķ�����
�ڣ����������ȼ�Ϊ����Ϊʹ����ij�տ�������Ϊ�Ż���Ϊ������Ӧ���Ƶ��쳵�������������������������������Ϊ��λ�������������ο���ʽ���ع�ֱ�ߵķ�����![]() ������
������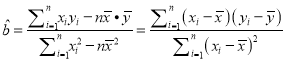 ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
��1���ֱ�����![]() ��
��![]() ������
������![]() �ϵļ�ֵ��
�ϵļ�ֵ��
��2����֤��������![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷ֲ�����ķ�����ijУѧ���г�ȡһ������Ϊ60�����������и߶��꼶��ȡ20�ˣ������꼶��ȡ25�ˣ���֪��У��һ�꼶����800�ˣ����Уѧ������Ϊ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������8�֣� ��֪������C��y=-x2+4x-3 ��
��1����������C�ڵ�A��0����3���͵�B��3��0���������ߵĽ������ꣻ
��2����������C�����ڵ�A�͵�B����������Χ�ɵ�ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��2sin��2x+�գ���|��|���У����� ![]() ����f��x����һ������������������ǣ� ��
����f��x����һ������������������ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ⱥ�2������һö���ӣ����õ��ĵ����ֱ��Ϊ![]() ��
�� ![]() .
.
��1����ֱ��![]() ��Բ
��Բ![]() ���еĸ��ʣ�
���еĸ��ʣ�
��2����![]() ��
�� ![]() ��5��ֵ�ֱ���Ϊ�����߶εij������������߶���Χ�ɵ��������εĸ���.
��5��ֵ�ֱ���Ϊ�����߶εij������������߶���Χ�ɵ��������εĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1����֪2sinx=sin�� ![]() ��x������
��x������ ![]() ��ֵ��
��ֵ��
��2������f��x��=ln��sinx�� ![]() ��+
��+ ![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com