
 如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.分析 (1)欲证FB=FC,可证∠FBC=∠FCB.由A、C、B、F四点共圆可知∠FBC=∠CAD,又同弧所对的圆周角相等,则∠FCB=∠FAB,而∠FAB=∠EAD,则∠FCB=∠EAD,AD是△ABC外角∠EAC的平分线,得∠CAD=∠EAD,故∠FBC=∠FCB;
(2)由(1)知,求FB的长,即可以转化为求FC的长,联系已知条件:告诉FA与AD的长度,即可证△FAC∽△FCD.
解答 (1)证明:∵A、C、B、F四点共圆
∴∠FBC=∠DAC
又∵AD平分∠EAC
∴∠EAD=∠DAC
又∵∠FCB=∠FAB(同弧所对的圆周角相等),∠FAB=∠EAD
∴∠FBC=∠FCB
∴FB=FC;
(2)解:∵∠BAC=∠BFC,∠FAB=∠FCB=∠FBC
∴∠FCD=∠BFC+∠FBC=∠BAC+∠FAB=∠FAC
∵∠AFC=∠CFD,
∴△FAC∽△FCD
∴FA:FC=FC:FD
∴FB2=FC2=FA•FD=16,
∴FB=4.
点评 本题主要考查了圆周角定理及相似三角形的判定.在圆中,经常利用同弧或者等弧所对的圆周角相等来实现角度的等量转化.还要善于将已知条件与所要求的问题集中到两个三角形中,运用三角形相似来解决问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
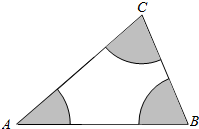 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
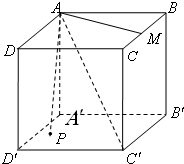 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段圆弧 | B. | 一段椭圆弧 | C. | 一段双曲线弧 | D. | 一段抛物线弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\frac{1+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
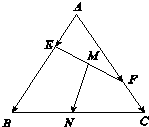 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com