
分析 (Ⅰ)由余弦定理及已知可得:$2c•\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=2a+b$,整理后可求cosC的值,结合范围C∈(0,π),即可得解C的值.
(Ⅱ)利用三角形面积公式及已知可得$S=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{4}ab$,利用基本不等式即可求得$\sqrt{ab}≥8,ab≥64$,从而得解.
解答 (本题满分为12分)
解:(Ⅰ)在△ABC中,由余弦定理可得:$2c•\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=2a+b$,
整理可得:a2+b2-c2=-ab,…3分
故$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=-\frac{1}{2}$,…5分
因为C∈(0,π),故$C=\frac{2π}{3}$…6分
(Ⅱ)因为$S=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{4}ab$,
故$\frac{{\sqrt{3}}}{4}ab=\sqrt{3}(a+b)≥2\sqrt{3}\sqrt{ab}$…10分
化简得$\sqrt{ab}≥8,ab≥64$…11分
当且仅当a=b=8时等号成立.
所以ab的最小值为64.…12分.
点评 本题主要考查了余弦定理,三角形面积公式,基本不等式在解三角形中的应用,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
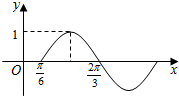 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,+∞) | B. | [2,+∞) | C. | [1,+∞) | D. | [0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com