
P为正方体ABCD-A1B1C1D1对角线BD1上的一点,且BP=λBD1(λ∈(0,1)).下面结论:
①A1D⊥C1P;
②若BD1⊥平面PAC,则λ=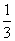 ;
;
③若△PAC为钝角三角形,则λ∈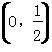 ;
;
④若λ∈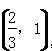 ,则△PAC为锐角三角形.
,则△PAC为锐角三角形.
其中正确的结论为________.(写出所有正确结论的序号)
①②④
[解析] 在正方体中,易证A1D⊥平面AD1C1B,又C1P⊂平面AD1C1B,所以A1D⊥C1P,①正确;若BD1⊥平面PAC,则点P为平面ACB1与体对角线BD1的交点,利用等体积法可得BP=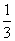 BD1,即λ=
BD1,即λ=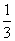 ,②正确;以点D为坐标原点,DA,DC,DD1所在射线分别为x轴、y轴、z轴的正半轴建立空间直角坐标系,设正方体的边长为1,则A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),又BP=λBD1,所以P(1-λ,1-λ,λ),若△PAC为钝角三角形,只能是∠APC是钝角,所以
,②正确;以点D为坐标原点,DA,DC,DD1所在射线分别为x轴、y轴、z轴的正半轴建立空间直角坐标系,设正方体的边长为1,则A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),又BP=λBD1,所以P(1-λ,1-λ,λ),若△PAC为钝角三角形,只能是∠APC是钝角,所以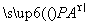 ·
·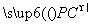 =(λ,λ-1,-λ)·(λ-1,λ,-λ)=3λ2-2λ<0,解得λ∈
=(λ,λ-1,-λ)·(λ-1,λ,-λ)=3λ2-2λ<0,解得λ∈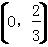 ,所以③错误;由③可知若λ∈
,所以③错误;由③可知若λ∈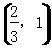 ,则△PAC为锐角三角形,④正确.所以正确的结论序号为①②④.
,则△PAC为锐角三角形,④正确.所以正确的结论序号为①②④.


科目:高中数学 来源: 题型:
等差数列{an}中,如果a1+a4+a7=39,a3+a6+a9=27,则数列{an}前9项的和为( )
A.297 B.144
C.99 D.66
查看答案和解析>>
科目:高中数学 来源: 题型:
在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列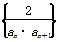 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-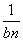 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在等腰直角三角形ABC中,斜边BC=2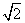 ,过点A作BC的垂线,垂足为A1,过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;…,依此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.
,过点A作BC的垂线,垂足为A1,过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;…,依此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是一容量为100的样本的质量的频率分布直方图,样本质量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本质量落在[15,20]内的频数为( )

A.10 B.20 C.30 D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com