
分析 若区间[1,2]为函数f(x)=|2x-t|的“不动区间”,则函数f(x)=|2x-t|和函数F(x)=|2-x-t|在[1,2]上单调性相同,则(2x-t)(2-x-t)≤0在[1,2]上恒成立,进而得到答案.
解答 解:∵函数y=f(x)与y=F(x)的图象关于y轴对称,
∴F(x)=f(-x)=|2-x-t|,
∵区间[1,2]为函数f(x)=|2x-t|的“不动区间”,
∴函数f(x)=|2x-t|和函数F(x)=|2-x-t|在[1,2]上单调性相同,
∵y=2x-t和函数y=2-x-t的单调性相反,
∴(2x-t)(2-x-t)≤0在[1,2]上恒成立,
即1-t(2x+2-x)+t2≤0在[1,2]上恒成立,
即2-x≤t≤2x在[1,2]上恒成立,
即有$\frac{1}{2}$≤t≤2;
即实数t的最大值为2;
故答案为:2.
点评 本题考查函数恒成立问题,涉及指数函数的图象和性质,正确理解不动区间的定义,是解答的关键.


科目:高中数学 来源: 题型:选择题
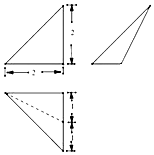
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1) | C. | (0,+∞) | D. | $(-∞,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
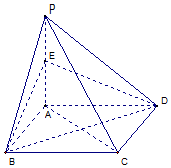 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com