
如图,椭圆C0: (a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.

(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=t22与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:t12+t22为定值.
(1) (x<-a,y<0) (2)见解析
(x<-a,y<0) (2)见解析
【解析】(1)解 设A(x1,y1),B(x1,-y1),
又知A1(-a,0),A2(a,0),
则直线A1A的方程为y= (x+a),①
(x+a),①
直线A2B的方程为y= (x-a).②
(x-a).②
由①②得y2= (x2-a2).③
(x2-a2).③
由点A(x1,y1)在椭圆C0上,故 .
.
从而y12=b2 ,
,
代入③得 (x<-a,y<0).
(x<-a,y<0).
(2)证明 设A′(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等,得4|x1||y1|=4|x2||y2|,
故x12y12=x22y22.
因为点A,A′均在椭圆上,
所以b2x12 =b2x22
=b2x22 .
.
由t1≠t2,知x1≠x2,所以x12+x22=a2.从而y12+y22=b2,
因此t12+t22=a2+b2为定值.


科目:高中数学 来源:2014高考名师推荐数学文科不等式恒成立问题(解析版) 题型:选择题
若当P(m,n)为圆 上任意一点时,不等式
上任意一点时,不等式 恒成立,则c的取值范围是( )
恒成立,则c的取值范围是( )
A. 
B. 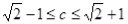
C. 
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD,则在三棱锥A—BCD中,下列命题正确的是( )

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设F1、F2分别是椭圆 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A. B.
B.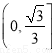 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设m、n是不同的直线,α、β是不同的平面,下列四个命题中正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥β,n⊥β,则m∥n
C.若α⊥β,m?α,则m⊥β
D.若m?α,n?α,m∥β,n∥β,则α∥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:解答题
设函数f(x)=sin xcos x- cos(π+x)cos x(x∈R).
cos(π+x)cos x(x∈R).
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b= 平移后得到函数y=g(x)的图象,求y=g(x)在[0,
平移后得到函数y=g(x)的图象,求y=g(x)在[0, ]上的最大值.
]上的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:选择题
以双曲线 (a>0,b>0)的左焦点F为圆心,作半径为b的圆F,则圆F与双曲线的渐近线( )
(a>0,b>0)的左焦点F为圆心,作半径为b的圆F,则圆F与双曲线的渐近线( )
A.相交 B.相离 C.相切 D.不确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:填空题
平面上有三个点A(-2,y),B ,C(x,y),若
,C(x,y),若 ⊥
⊥ ,则动点C的轨迹方程为__________.
,则动点C的轨迹方程为__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(一)(解析版) 题型:解答题
设集合A={x|x2<4},B={x|1<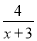 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com