
分析 (1)当a=$\frac{1}{4}$时,不等式f(x)<0变为(x-1)(x-2)<0,解得1<x<2,即可.
(2)f(1)+$\frac{1}{a}$=-(1-4a)+$\frac{1}{a}$=4a+$\frac{1}{a}$-1$≥2\sqrt{4a•\frac{1}{a}}-1$=3(当4a=$\frac{1}{a}$,即a=$\frac{1}{2}$时取等号).
解答 解:(1)当a=$\frac{1}{4}$时,不等式f(x)<0变为(x-1)(x-2)<0,
解得1<x<2,即原不等式解集为{x|1<x<2}.
(2)∵a>0,∴f(1)+$\frac{1}{a}$=-(1-4a)+$\frac{1}{a}$=4a+$\frac{1}{a}$-1$≥2\sqrt{4a•\frac{1}{a}}-1$=3
即当4a=$\frac{1}{a}$,即a=$\frac{1}{2}$时,f(1)+$\frac{1}{a}$的最小值为3.
点评 本题考查了二次不等式的解法、均值不等式的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在正方体ABCD-A1B1C1D1中,O、O1分别为底面ABCD和A1B1C1D1的中心,以OO1所在直线为轴旋转线段BC1形成的几何体的正视图为( )
在正方体ABCD-A1B1C1D1中,O、O1分别为底面ABCD和A1B1C1D1的中心,以OO1所在直线为轴旋转线段BC1形成的几何体的正视图为( )| A. |  | B. |  | C. | 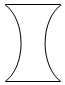 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
| 有兴趣 | 无兴趣 | 合计 | |
| 男 | 25 | 5 | 30 |
| 女 | 15 | 15 | 30 |
| 合计 | 40 | 20 | 60 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个社会调查机构就某地居民的月收入调查了100人,并根据所得数据画出了如图所示的频率分布直方图,则估计这100人的月平均收入为2400元.
一个社会调查机构就某地居民的月收入调查了100人,并根据所得数据画出了如图所示的频率分布直方图,则估计这100人的月平均收入为2400元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2-1 | B. | 1-ln2 | C. | ln2 | D. | -ln2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com