
分析 (1)根据正弦定理和余弦定理求出C的值即可;(2)整理f(A),根据A的范围,求出f(A)的最大值即可.
解答 解:(1)由$\frac{sinB}{sinA+sinC}$=$\frac{c+b-a}{c+b}$,
由正弦定理得:$\frac{b}{a+c}$=$\frac{c+b-a}{c+b}$,化简即为a2+b2-c2=ab,
再由余弦定理可得cosC=$\frac{{a}^{2}{+c}^{2}{-c}^{2}}{2ab}$=$\frac{1}{2}$,
因为0<C<π,所以∠C=$\frac{π}{3}$;
(2)f(A)=1-2cos2A+2sinAcosA=$\sqrt{2}$sin(2A-$\frac{π}{4}$),
在锐角△ABC中,$\frac{π}{6}$<A<$\frac{π}{2}$,
$\frac{π}{12}$<2A-$\frac{π}{4}$<$\frac{3π}{4}$,
故当2A-$\frac{π}{4}$=$\frac{π}{2}$,A=$\frac{3π}{8}$时,
f(A)max=$\sqrt{2}$.
点评 本题考查了三角函数的性质,考查正弦定理和余弦定理的应用,是一道中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
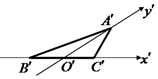 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\frac{{x}^{2}-x}{x}$与y=x-1 | C. | y=x,y=$\root{3}{{x}^{3}}$ | D. | y=|x|,y=($\sqrt{x}$)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com