【题目】已知某几何体的三视图如图2所示（小正方形的边长为
），则该几何体的外接球的表面积为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】分析：首先根据题中所给的三视图，还原几何体，得到该几何体是由正方体切割而成的，找到该几何体的顶点有三个是正方体的棱的中点，一个就是正方体的顶点，之后将几何体补体，从而得到该三棱锥的外接球是补成的棱柱的外接球，利用公式求得结果.
详解：根据题中所给的三视图，可以将几何体还原，可以得到该几何体是由正方体切割而成的，记正方体是
，
则记
的中点为E，CD中点为F，
中点为G，
题中所涉及的几何体就是三棱锥
，
经过分析，将几何体补体，
取棱
中点H，再取正方体的顶点
，
从而得到该三棱锥的外接球即为直三棱柱
的外接球，
利用正弦定理可以求得底面三角形的外接圆的半径为
，
棱柱的高为4，所以可以求得其外接球的半径
，
所以其表面积为
，故选A.
科目：高中数学 来源： 题型：
【题目】如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形.
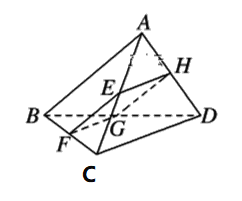
(1)求证：AB∥平面EFGH
(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为
=0.85x-85.71，则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心（
，
）
C. 若该大学某女生身高增加1cm，则其体重约增加0.85kg
D. 若该大学某女生身高为170cm，则可断定其体重比为58.79kg
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，
，
，且
，E为PD中点.
（I）求证：
平面ABCD；
（II）求二面角B-AE-C的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
的左、右焦点分别为
、
，
、
分别是双曲线左、右两支上关于坐标原点
对称的两点，且直线
的斜率为
.
、
分别为
、
的中点，若原点在以线段
为直径的圆上，则双曲线的离心率为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，已知四边形BCDE为直角梯形，
，
，且
，A为BE的中点
将
沿AD折到
位置
如图
，连结PC，PB构成一个四棱锥
．
Ⅰ
求证
；
Ⅱ若
平面ABCD．
求二面角
的大小；
在棱PC上存在点M，满足
，使得直线AM与平面PBC所成的角为
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出定义：若
（其中
为整数），则叫做离实数
最近的整数，记作
，即
.设函数
，二次函数
，若函数
与
的图象有且只有一个公共点，则
的取值不可能是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
