
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)=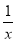 在(0,1]上解的个数.
在(0,1]上解的个数.
(1)[2,+∞).
(2)0
【解析】【解析】
(1)当a=1时,
f(x)=|x-2|+bln x
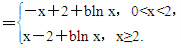
①当0<x<2时,f(x)=-x+2+bln x,
f′(x)=-1+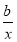 .
.
由条件得-1+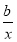 ≥0恒成立,即b≥x恒成立.
≥0恒成立,即b≥x恒成立.
所以b≥2;
②当x≥2时,f(x)=x-2+bln x,
f′(x)=1+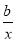 .
.
由条件得1+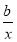 ≥0恒成立,即b≥-x恒成立.
≥0恒成立,即b≥-x恒成立.
所以b≥-2.
因为函数f(x)的图像在(0,+∞)上不间断,综合①②得b的取值范围是[2,+∞).
(2)令g(x)=|ax-2|+ln x-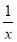 ,即
,即
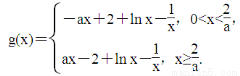
当0<x<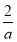 时,
时,
g(x)=-ax+2+ln x-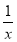 ,
,
g′(x)=-a+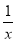 +
+ .
.
因为0<x<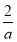 ,所以
,所以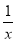 >
>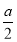 ,
,
则g′(x)>-a+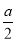 +
+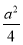 =
=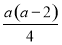 ≥0,
≥0,
即g′(x)>0,所以g(x)在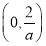 上是单调增函数;
上是单调增函数;
当x>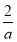 时,g(x)=ax-2+ln x-
时,g(x)=ax-2+ln x-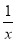 ,
,
g′(x)=a+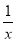 +
+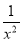 >0,
>0,
所以g(x)在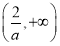 上是单调增函数.
上是单调增函数.
因为函数g(x)的图像在(0,+∞)上不间断,所以g(x)在(0,+∞)上是单调增函数.
因为g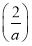 =ln
=ln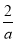 -
-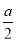 ,
,
而a≥2,所以ln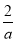 ≤0,则g
≤0,则g <0,
<0,
g(1)=|a-2|-1=a-3.
①当a≥3时,因为g(1)≥0,所以g(x)=0在(0,1]上有唯一解,即方程f(x)=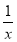 解的个数为1;
解的个数为1;
②当2≤a<3时,因为g(1)<0,所以g(x)=0在(0,1]上无解,即方程f(x)=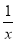 解的个数为0.
解的个数为0.


科目:高中数学 来源:2015届高考苏教数学(理)训练4 函数及其表示(解析版) 题型:填空题
根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为f(x)=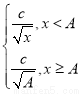 (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________.
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
已知cos θ·tan θ<0,那么角θ是第________象限角.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
设函数f(x)=ln x-ax,g(x)=ex-ax,其中a为实数.若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
设函数f(x)=ax2+bx+c(a,b,c∈R).若x=-1为函数f(x)ex的一个极值点,则下列图像不可能为y=f(x)图像的是________.(填写序号)
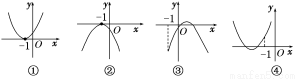
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
曲线f(x)=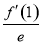 ·ex-f(0)x+
·ex-f(0)x+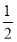 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练10 对数与对数函数(解析版) 题型:解答题
已知f(x)=logax(a>0且a≠1),如果对于任意的x∈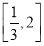 都有|f(x)|≤1成立,试求a的取值范围.
都有|f(x)|≤1成立,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:填空题
设m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若α∥β,m?β,n?α,则m∥n;
②若α∥β,m⊥β,n∥α,则m⊥n;
③若α⊥β,m⊥α,n∥β,则m∥n;
④若α⊥β,m⊥α,n⊥β,则m⊥n.
上面命题中,所有真命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com