
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据题意得A(-a,0),B(a,0).设P(m,n),利用直线的斜率公式算出kPA•kPB=$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$.由点P是双曲线上的点,坐标代入双曲线方程化简整理得n2=$\frac{{b}^{2}({m}^{2}-{a}^{2})}{{a}^{2}}$,从而得出kPA•kPB=$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,由此得到a、c的关系式,从而解出双曲线的离心率e的值.
解答 解:由题意,可得A(-a,0),B(a,0),设P(m,n)
∴kPA•kPB=$\frac{n-0}{m+a}•\frac{n-0}{m-a}$=$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$.
∵点P是双曲线上的点,可得$\frac{{m}^{2}}{{a}^{2}}-\frac{{n}^{2}}{{b}^{2}}=1$,化简整理得n2=$\frac{{b}^{2}({m}^{2}-{a}^{2})}{{a}^{2}}$.
∴kPA•kPB=$\frac{{b}^{2}}{{a}^{2}}$
∵kPA•kPB=$\frac{5}{4}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,可得e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{3}{2}$.
故选:C.
点评 本题给出双曲线满足的条件,求双曲线的离心率.着重考查了直线的斜率公式、双曲线的简单几何性质等知识,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{21}}{3}$ | B. | $\sqrt{13}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40π}{3}$ | B. | $\frac{50π}{3}$ | C. | 12π | D. | 15π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
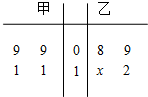 如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | $\frac{32π}{3}$ | C. | $\frac{20\sqrt{5}π}{3}$ | D. | 20π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com