
分析 (1)求出函数f(x)的导函数,由a>0,定义域为(0,+∞),再由f′(x)>0求得函数f(x)的单调增区间;
(2)当a<0时,求出导函数的零点-$\frac{1}{2a}$,1,分-$\frac{1}{2a}$>1,$\frac{1}{2}$≤-$\frac{1}{2a}$≤1,-$\frac{1}{2a}$<$\frac{1}{2}$,讨论函数f(x)在区间[$\frac{1}{2}$,1]上的单调性,求出函数的最小值,最后表示为关于a的分段函数;
(3)设出线段AB的中点M的坐标,得到N的坐标,由两点式求出AB的斜率,再由导数得到曲线C过N点的切线的斜率,由斜率相等得到ln $\frac{{x}_{2}}{{x}_{1}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$,令$\frac{{x}_{2}}{{x}_{1}}$=t后构造函数g(t)=lnt-$\frac{2(t-1)}{1+t}$(t>1),根据函数的单调性判断不成立.
解答 解:(1)∵f(x)=ax2+(1-2a)x-lnx,
∴f′(x)=2ax+(1-2a)-$\frac{1}{x}$=$\frac{(2ax+1)(x-1)}{x}$,
∵a>0,x>0,
∴2ax+1>0,解f′(x)>0,得x>1,
∴f(x)的单调增区间为(1,+∞);
(2)当a<0时,由f′(x)=0,得x1=-$\frac{1}{2a}$,x2=1,
①当-$\frac{1}{2a}$>1,即-$\frac{1}{2}$<a<0时,f(x)在(0,1)上是减函数,
∴f(x)在[$\frac{1}{2}$,1]上的最小值为f(1)=1-a.
②当$\frac{1}{2}$≤-$\frac{1}{2a}$≤1,即-1≤a≤-$\frac{1}{2}$时,
f(x)在[$\frac{1}{2}$,-$\frac{1}{2a}$]上是减函数,在[-$\frac{1}{2a}$,1]上是增函数,
∴f(x)的最小值为f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
③当-$\frac{1}{2a}$<$\frac{1}{2}$,即a<-1时,f(x)在[$\frac{1}{2}$,1]上是增函数,
∴f(x)的最小值为f($\frac{1}{2}$)=$\frac{1}{2}$-$\frac{3}{4}$a+ln2.
综上,函数f(x)在区间[$\frac{1}{2}$,1]上的最小值为:
f(x)min=$\left\{\begin{array}{l}{\frac{1}{2}-\frac{3}{4}a+ln2,a<-1}\\{1-\frac{1}{4a}+ln(-2a),-1≤a≤-\frac{1}{2}}\\{1-a,-\frac{1}{2}<a<0}\end{array}\right.$;
(3)设M(x0,y0),则点N的横坐标为x0=$\frac{{{x}_{1}+x}_{2}}{2}$,
直线AB的斜率k1=$\frac{{{y}_{1}-y}_{2}}{{{x}_{1}-x}_{2}}$=$\frac{1}{{{x}_{1}-x}_{2}}$[a(x12-x22)+(1-2a)(x1-x2)+lnx2-lnx1]
=a(x1+x2)+(1-2a)+$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{1}-x}_{2}}$,
曲线C在点N处的切线斜率k2=f′(x0)=2ax0+(1-2a)-$\frac{1}{{x}_{0}}$=a(x1+x2)+(1-2a)-$\frac{2}{{{x}_{1}+x}_{2}}$,
假设曲线C在点N处的切线平行于直线AB,则k1=k2,
即 $\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{1}-x}_{2}}$=-$\frac{2}{{{x}_{1}+x}_{2}}$,
∴ln $\frac{{x}_{2}}{{x}_{1}}$=$\frac{2({{x}_{2}-x}_{1})}{{{x}_{1}+x}_{2}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$,
不妨设x1<x2,$\frac{{x}_{2}}{{x}_{1}}$=t>1,则lnt=$\frac{2(t-1)}{1+t}$,
令g(t)=lnt-$\frac{2(t-1)}{1+t}$(t>1),则g′(t)=$\frac{1}{t}$-$\frac{4}{{(1+t)}^{2}}$=$\frac{{(t-1)}^{2}}{{t(1+t)}^{2}}$>0,
∴g(t)在(1,+∞)上是增函数,又g(1)=0,
∴g(t)>0,即lnt=$\frac{2(t-1)}{1+t}$不成立,
∴曲线C在点N处的切线不平行于直线AB.
点评 本题考查利用导数求函数的单调区间,考查了利用导数求函数的最值,体现了分类讨论的数学思想方法,训练了利用构造函数法证明等式恒成立问题,特别是对于(3)的证明,要求学生较强的应变能力,是压轴题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$ | B. | $\frac{{9{x^2}}}{8}+\frac{{16{y^2}}}{9}=1$ | C. | $\frac{{8{x^2}}}{9}+\frac{{9{y^2}}}{16}=1$ | D. | $\frac{{9{x^2}}}{8}+\frac{{9{y^2}}}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
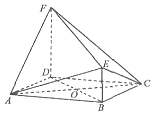 如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
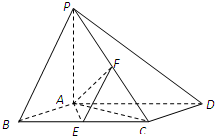 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com