
分析 (1)根据两角和差的余弦公式即可得到$\left\{\begin{array}{l}{cosαcosβ-sinαsinβ=-\frac{3}{5}}\\{cosαcosβ+sinαsinβ=\frac{1}{5}}\end{array}\right.$,从而可解出sinαsinβ和cosαcosβ的值,从而求出tanα•tanβ的值;
(2)根据条件可以求出$tan(A+B)=-\frac{3}{4}$,从而$\frac{tanA+tanB}{1-tanAtanB}=-\frac{3}{4}$,结合tanA=2tanB即可求出$tanA=2+\sqrt{6},tanB=\frac{2+\sqrt{6}}{2}$,这样设AB边上的高为CD,从而由$AB=\frac{CD}{tanA}+\frac{CD}{tanB}$及AB=3即可求出CD的值,从而得出△ABC的面积.
解答 解:(1)$cos(α+β)=-\frac{3}{5}$,$cos(α-β)=\frac{1}{5}$;
∴$\left\{\begin{array}{l}{cosαcosβ-sinαsinβ=-\frac{3}{5}}\\{cosαcosβ+sinαsinβ=\frac{1}{5}}\end{array}\right.$;
∴$\left\{\begin{array}{l}{sinαsinβ=\frac{2}{5}}\\{cosαcosβ=-\frac{1}{5}}\end{array}\right.$;
∴tanαtanβ=-2;
(2)△ABC为锐角三角形;
∴$\frac{π}{2}<A+B<π$,$sin(A+B)=\frac{3}{5}$;
∴$cos(A+B)=-\frac{4}{5}$;
∴$tan(A+B)=-\frac{3}{4}$;
∴$\frac{tanA+tanB}{1-tanAtanB}=-\frac{3}{4}$,且tanA=2tanB;
∴$\frac{2tanB+tanB}{1-2ta{n}^{2}B}=-\frac{3}{4}$,整理得:2tan2B-4tanB-1=0;
解得$tanB=\frac{2+\sqrt{6}}{2}$或$\frac{2-\sqrt{6}}{2}$(舍去),则$tanA=2+\sqrt{6}$,
如图,设AB边上的高为CD,则: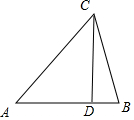 $AB=AD+DB=\frac{CD}{tanA}+\frac{CD}{tanB}=\frac{3CD}{2+\sqrt{6}}$,且AB=3;
$AB=AD+DB=\frac{CD}{tanA}+\frac{CD}{tanB}=\frac{3CD}{2+\sqrt{6}}$,且AB=3;
∴$CD=2+\sqrt{6}$;
∴${S}_{△ABC}=\frac{1}{2}×3×(2+\sqrt{6})=\frac{6+3\sqrt{6}}{2}$.
点评 考查两角和差的余弦和正切公式,弦化切公式,一元二次方程的解法,以及正切函数的定义,三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1-\sqrt{5}}{4}$,0) | B. | ($\frac{1-\sqrt{5}}{4}$,$\frac{\sqrt{5}-2}{2}$) | C. | [$\frac{9-9\sqrt{5}}{32}$,$\frac{\sqrt{5}-2}{2}$) | D. | [$\frac{9-9\sqrt{5}}{32}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
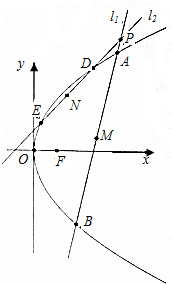 已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.
已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8) | B. | (-∞,-8]∪(0,1) | C. | (-∞,-8]∪[0,1] | D. | (-8,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com