Question

10．正方体ABCD-A₁B₁C₁D₁的棱长为6，点O在BC上，且BO=OC，过点O的直线l与直线AA₁，C₁D₁分别交于M，N两点，则MN与面ADD₁A₁所成角的正弦值为（　　）

• A． $\frac{2}{3}$
• B． $\frac{\sqrt{3}}{2}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\frac{\sqrt{3}}{3}$

Answer 1

分析 设MD₁交AD于E，根据C₁D₁∥平面ABCD可得C₁D₁∥OE，从而E为AD的中点，故可计算出MD₁和ND₁，从而可求出sin∠NMD₁．

解答 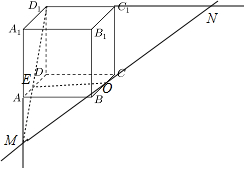解：∵C₁D₁⊥平面ADD₁A₁，
∴∠NMD₁是MN与面ADD₁A₁所成角，
设MD₁与AD交点为E，连结OE，
∵C₁D₁∥平面ABCD，C₁D₁?平面MND₁，平面MND₁∩平面ABCD=DE，
∴C₁D₁∥OE，
∵O是BC的中点，∴E是AD的中点，
∴E是MD₁的中点，MD₁=2ED₁=6$\sqrt{5}$，
∴ND₁=2OE=12，∴MN=$\sqrt{1{2}^{2}+（6\sqrt{5}）^{2}}$=18，
∴sin∠NMD₁=$\frac{N{D}_{1}}{MN}$=$\frac{2}{3}$．
故选A．

点评 本题考查了线面平行的性质，线面角的计算，属于中档题．