
已知点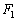 、
、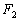 为双曲线
为双曲线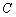 :
: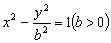 的左、右焦点,过
的左、右焦点,过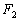 作垂直于
作垂直于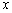 轴的直线,在
轴的直线,在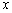 轴上方交双曲线
轴上方交双曲线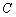 于点
于点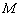 ,且
,且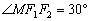 .圆
.圆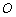 的方程是
的方程是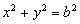 .
.
(1)求双曲线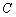 的方程;
的方程;
(2)过双曲线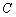 上任意一点
上任意一点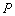 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为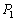 、
、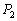 ,求
,求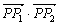 的值;
的值;
(3)过圆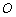 上任意一点
上任意一点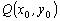 作圆
作圆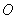 的切线
的切线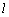 交双曲线
交双曲线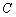 于
于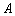 、
、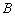 两点,
两点,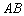 中点为
中点为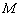 ,求证:
,求证: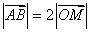 .
.
科目:高中数学 来源: 题型:
寒假期间,我市某校学生会组织部分同学,用“10分制”随机调查“阳光花园”社区人们的幸福度,现从调查人群中随机抽取16名,如果所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶);若幸福度分数不低于8.5分,则该人的幸福度为“幸 福”.
福”.
(I)求从这16人中随机选取3 人,至少有2人为“幸福”的概率;
人,至少有2人为“幸福”的概率;
(II)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记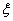 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求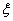 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
设无穷等比数列 的公比为q,且
的公比为q,且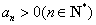 ,
,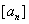 表示不超过实数
表示不超过实数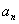 的最大整数(如
的最大整数(如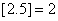 ),记
),记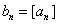 ,数列
,数列 的前
的前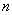 项和为
项和为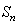 ,数列
,数列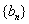 的前
的前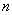 项和为
项和为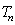 .
.
(Ⅰ)若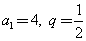 ,求
,求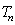 ;
;
(Ⅱ)若对于任意不超过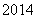 的正整数n,都有
的正整数n,都有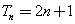 ,证明:
,证明: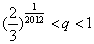 .
.
(Ⅲ)证明: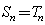 (
(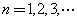 )的充分必要条件为
)的充分必要条件为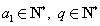 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知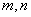 是不重合的直线,
是不重合的直线,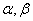 是不重合的平面,有下列命题:
是不重合的平面,有下列命题:
①若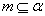 ,
,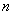 ∥
∥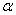 ,则
,则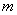 ∥
∥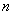 ;
;
②若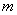 ∥
∥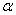 ,
,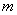 ∥
∥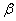 ,则
,则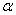 ∥
∥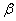 ;
;
③若 ,
,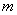 ∥
∥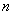 ,则
,则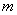 ∥
∥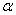 且
且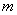 ∥
∥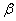 ;
;
④若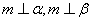 ,则
,则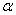 ∥
∥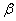
其中真命题的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com