
分析 根据题意画出图形,结合图形利用勾股定理即可求出图象上的一个最高点和其相邻最低点的距离的最小值.
解答 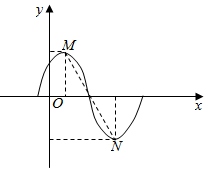 解:如图所示
解:如图所示
函数y=asin(ax+θ)(a>0,θ≠0)图象上的一个最高点M
和其相邻最低点N的距离的最小值为:
|MN|=$\sqrt{{(2a)}^{2}{+(\frac{π}{a})}^{2}}$=$\sqrt{{4a}^{2}+\frac{{π}^{2}}{{a}^{2}}}$≥$\sqrt{2\sqrt{{4a}^{2}•\frac{{π}^{2}}{{a}^{2}}}}$=2$\sqrt{π}$,
当且仅当4a2=$\frac{{π}^{2}}{{a}^{2}}$,即a=$\frac{π}{2}$时取“=”.
故答案为:2$\sqrt{π}$.
点评 本题考查了函数y=Asin(ωx+φ)的图象与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,+∞) | C. | [-2,$\frac{7}{6}$) | D. | (-2,-$\frac{7}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )
某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )| A. | 80 | B. | 90 | C. | 120 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
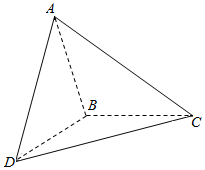 三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.
三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x | B. | y=2|sinx| | C. | y=($\frac{1}{3}$)cosx | D. | y=tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com