Question

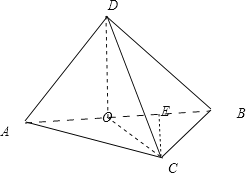
【题目】将一副斜边长相等的直角三角板拼接成如图所示的空间图形，其中，.若将它们的斜边重合，让三角形以为轴转动，则下列说法不正确的是（ ）

A. 当平面平面时，，两点间的距离为

B. 当平面平面时，与平面所成的角为

C. 在三角形转动过程中，总有

D. 在三角形转动过程中，三棱锥的体积最大可达到

Answer 1

【答案】C

【解析】分析：A选项，结合图象，利用面面垂直的性质及直角三角形斜边上的中线长等于斜边长的一半求解；B选项，先作出与平面所成的角，再求得其为；C选项用反证法，假设垂直，根据线面垂直的判定与性质推到是否可能，从而得出结论；D选项根据棱锥的体积公式，在底面积不变的情况下，体积的大小取决于高，当平面ABD⊥平面ABC时，高最大，求出即可．

详解：A选项，取AB中点O，连接DO、CO，

∵AD=BD=，∴DO=1，AB=2，OC=1

∵平面ABD⊥平面ABC，DO⊥AB，∴DO⊥平面ABC，DO⊥OC，

∴DC=，A选项正确；

B选项，过点D作DM⊥AB，连接MC，则∠DCM就是与平面所成的角，因为DM=CM,所以∠DCM=45°，所以B选项正确；

C选项，若AB⊥CD，则AB⊥平面CDO，AB⊥OC，∵O为中点，∴AC=BC，∠BAC=45°与∠BAC=30°矛盾，∴C选项错误；

D选项，当DO⊥平面ABC时，棱锥的高最大，此时V棱锥=×AC×BC×DO=××1×1=．D选项正确．

故答案为：C