练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．从1，2，3，4四个数字中任取两个不同数字，则这两个数字之积小于5的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．$\frac{5}{6}$

    分析 首先明确所有的事件数已经满足两个数字之积小于5的事件数，路古典概型的公式求概率．

    解答 解：从1，2，3，4四个数字中任取两个不同数字共有${C}_{4}^{2}$=6种取法，
    这两个数字之积小于5的事件有12，13，14共有3种，
    由古典概型公式得从1，2，3，4四个数字中任取两个不同数字，
    则这两个数字之积小于5的概率为到$\frac{3}{6}=\frac{1}{2}$；
    故选B．

    点评 本题考查了古典概型的概率求法；关键是明确所有事件以及满足条件的事件数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

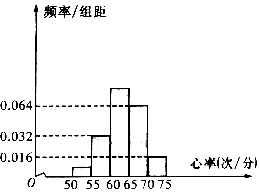    19．某学校的特长班有50名学生，其中有体育生20人，艺术生30名，在学校组织的一次体检中，该班所有学生进行了心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60），…，第五组[70，75），按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．
    （1）求a的值，并求这50名学生心率的平均数；
    （2）因为学习专业的原因，体育生常年进行系统的身体锻炼，艺术生则很少进行系统的身体锻炼，若从第一组和第二组的学生中随机抽取一名，该学生是体育生的概率为0.8，请将下面的列联表补充完整，并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关？请说明理由．
    参考数据：
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
    心率小于60次/分心率不小于60次/分合计
    体育生81220
    艺术生22830
    合计104050

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数$f（x）=sin（{ωx+\frac{π}{6}}）（{0＜ω＜2}）$满足条件：$f（{-\frac{1}{2}}）=0$，为了得到y=f（x）的图象，可将函数g（x）=cosωx的图象向右平移m个单位（m＞0），则m的最小值为（　　）
    A．1B．$\frac{1}{2}$C．$\frac{π}{6}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=lnx+（1-a）x3+bx，g（x）=xex-b（a，b∈R，e为自然对数的底数），且f（x）在点（e，f（e））处的切线方程为y=（$\frac{1}{e}$+1）x
    （Ⅰ）求实数a，b的值；
    （Ⅱ）求证：f（x）≤g（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

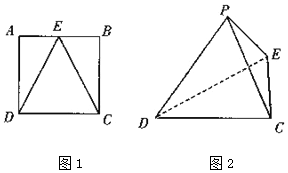    4．如图1，2，E是正方形ABCD的AB边的中点，将△AED与△BEC分别沿ED、EC折起，使得点A与点B重合，记为点P，得到三棱锥P-CDE．
    （Ⅰ）求证：平面PED⊥平面PCD；
    （Ⅱ）求二面角P-CE-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在△ABC中，AB=8，BC=7，AC=5，则AB边上的高是$\frac{5\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．数列{an}的前n项和为Sn，Sn=（2n-1）an，且a1=1．
    （1）求数列{an}的通项公式；
    （2）若bn=nan，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数f（x）=|x+2|-|x-2|，g（x）=x+$\frac{1}{2}$．
    （Ⅰ）求不等式f（x）≥g（x）的解集；
    （Ⅱ）若?x∈R，f（x）≥t2-5t恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在平面直角坐标系xOy内，动点M（x，y）与两定点（-2，0），（2，0）连线的斜率之积为-$\frac{1}{4}$．
    （1）求动点M的轨迹C的方程；
    （2）设点A（x1，y1），B（x2，y2）是轨迹C上相异的两点．
    （Ⅰ）过点A，B分别作抛物线y2=4$\sqrt{3}$x的切线l1，l2，l1与l2两条切线相交于点$N（{-\sqrt{3}，t}）$，证明：$\overrightarrow{NA}•\overrightarrow{NB}$=0；
    （Ⅱ）若直线OA与直线OB的斜率之积为-$\frac{1}{4}$，证明：S△AOB为定值，并求出这个定值．

    查看答案和解析>>

    同步练习册答案