
分析 (1)由离心率e=$\frac{{\sqrt{3}}}{2}$,可得a2=4b2,由过点F 垂直于x轴的直线被椭圆所截得弦长为1,可得$\frac{2{b}^{2}}{a}$=1,解出即可得出.
(2)点M(m,-2),A(0,1),B(0,-1).直线MA方程为:y=-$\frac{3}{m}$x+1,直线MB方程为:y=-$\frac{1}{m}$x-1.
分别与椭圆$\frac{{x}^{2}}{4}+{y}^{2}$=1联立方程组,可得:$(\frac{36}{{m}^{2}}+1){x}^{2}-\frac{24}{m}x$=0,$(\frac{4}{{m}^{2}}+1){x}^{2}+\frac{8}{m}x$=0,解得xP,xQ,可得yP,yQ.P,Q坐标.可得直线PQ方程,即可证明.
解答 (1)解:由离心率e=$\frac{{\sqrt{3}}}{2}$,可得a2=4b2,
∵过点F 垂直于x轴的直线被椭圆所截得弦长为1,∴$\frac{2{b}^{2}}{a}$=1,
解得b=1,a=4,
∴椭圆C方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)证明:点M(m,-2),A(0,1),B(0,-1).
直线MA方程为:y=-$\frac{3}{m}$x+1,
直线MB方程为:y=-$\frac{1}{m}$x-1.
分别与椭圆$\frac{{x}^{2}}{4}+{y}^{2}$=1联立方程组,可得:$(\frac{36}{{m}^{2}}+1){x}^{2}-\frac{24}{m}x$=0,$(\frac{4}{{m}^{2}}+1){x}^{2}+\frac{8}{m}x$=0,
解得xP=$\frac{24m}{{m}^{2}+36}$,xQ=$\frac{-8m}{{m}^{2}+4}$,
可得:yP=-$\frac{3}{m}$xP+1=$\frac{{m}^{2}-36}{{m}^{2}+36}$,同理可得yQ=$\frac{4-{m}^{2}}{4+{m}^{2}}$.
∴P$(\frac{24m}{{m}^{2}+36},\frac{{m}^{2}-36}{{m}^{2}+36})$,Q$(\frac{-8m}{{m}^{2}+4},\frac{4-{m}^{2}}{{m}^{2}+4})$.
直线PQ的斜率k=$\frac{{m}^{2}-12}{16m}$,
则直线PQ方程为:y-$\frac{4-{m}^{2}}{4+{m}^{2}}$=$\frac{{m}^{2}-12}{16m}$$(x+\frac{8m}{{m}^{2}+4})$.
化简可得直线PQ的方程为:y═$\frac{{m}^{2}-12}{16m}$x-$\frac{1}{2}$.
∴直线PQ恒过定点$(0,-\frac{1}{2})$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
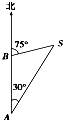 (文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.
(文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真,假,真 | B. | 假,假,真 | C. | 真,真,假 | D. | 假,假,假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx2,g(x)=2lgx | B. | y=f(x),y=f(x+1) | ||
| C. | $f(u)=\sqrt{\frac{1+u}{1-u}},f(v)=\sqrt{\frac{1+v}{1-v}}$ | D. | $f(x)=x,g(x)=\sqrt{x^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com