
| ${e^{\frac{π}{314}}}$ | ${e^{-\frac{π}{314}}}$ | ${e^{\frac{78π}{314}}}$ | ${e^{-\frac{78π}{314}}}$ | ${e^{\frac{79π}{314}}}$ | ${e^{-\frac{79π}{314}}}$ |
| 1.010 | 0.990 | 2.182 | 0.458 | 2.204 | 0.454 |
分析 (1)求出函数的导数,根据f′(0)=0,求出φ的值即可;
(2)求出函数的导数,根据函数的单调性求出a的范围即可;
(3)根据三角函数的性质累加即可.
解答 解:(1)$f'(x)=\sqrt{2}cos({x+φ})-{e^{-x}},f'(0)=\sqrt{2}cosφ-1=0$,则$φ=\frac{π}{4}$;
(2)$f(x)=\sqrt{2}sin({x+\frac{π}{4}})-a+{e^{-x}}≤0$,即$g(x)=({\sqrt{2}sin({x+\frac{π}{4}})-a}){e^x}+1≤0$恒成立,
g(0)=-a+2≤0,则a≥2,
$g'(x)=({\sqrt{2}sin({x+\frac{π}{4}})-a+\sqrt{2}cos({x+\frac{π}{4}})}){e^x}=({2cosx-a}){e^x}≤0$,
则g(x)递减.
所以a≥2时,$g(x)=({\sqrt{2}sin({x+\frac{π}{4}})-a}){e^x}+1≤g(0)=-a+2≤0$;
(3)证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}}=1+\sum_{k=1}^{78}{({sin\frac{kπ}{314}+sin\frac{{({157-k})π}}{314}})}$
=$1+\sum_{k=1}^{78}{\sqrt{2}sin({\frac{kπ}{314}+\frac{π}{4}})<1}+\sum_{k=1}^{78}{({2-{e^{-\frac{kπ}{314}}}})}=157-\sum_{k=1}^{78}{{e^{-\frac{kπ}{314}}}}$
=$157-\frac{{{e^{-\frac{π}{314}}}({1-{e^{-\frac{78π}{314}}}})}}{{1-{e^{-\frac{π}{314}}}}}=157-\frac{{1-{e^{-\frac{78π}{314}}}}}{{{e^{\frac{π}{314}}}-1}}<157-\frac{1-0.4585}{0.0105}=105\frac{3}{7}<106$.
点评 本题考查了三角函数的性质,考查函数的单调性问题,考查不等式的证明,是一道综合题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | x=0或$x=\frac{1}{2}$ | B. | x=-2或x=0 | C. | $x=\frac{1}{2}$ | D. | x=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{3}{2},3)$ | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},\frac{3}{2}]$ | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
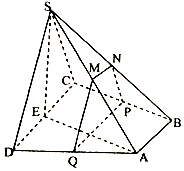 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com