Question

20．已知直线a⊥直线b，b⊥直线c，c⊥a，直线l与a，b所成的角分别为45°，60°，则l与c所成的角为（　　）

• A． 90°
• B． 60°
• C． 45°
• D． 30°

Answer 1

分析 以直线a所在直线为x轴，以直线c所在直线为y轴，以直线b所在直线为z轴，建立空间直角坐标系，建立空间直角坐标系，利用向量法能求出l与b的夹角．

解答 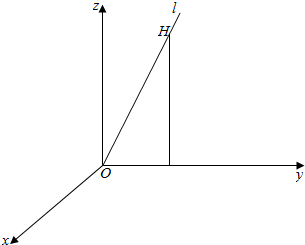解：∵直线a⊥直线b，b⊥直线c，c⊥a，
∴假设a，b，c交于点O，且两两垂直，
以直线a所在直线为x轴，以直线c所在直线为y轴，
以直线b所在直线为z轴，建立空间直角坐标系，建立空间直角坐标系，
在直线l上取一点H（x，y，z），
∵直线l与a，b所成的角分别为45°，60°，
∴x=cos60°$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$，y=cos45°$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$，
∴${x}^{2}+{y}^{2}=\frac{3}{4}（{x}^{2}+{y}^{2}+{z}^{2}）$，
∴z${\;}^{2}=\frac{1}{4}（{x}^{2}+{y}^{2}+{z}^{2}）$，
∴z=cos60°$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$，
∴l与b的夹角为60°．
故选：B．

点评 本题考查异面直线所成角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．