Question

9．设P是圆x²+y²=a²（a＞0）上的动点，点D是点P在x轴上的投影，M为PD上一点，且$\overrightarrow{MD}=\frac{b}{a}\overrightarrow{PD}$（a＞b＞0）．
（Ⅰ）求证：点M的轨迹Γ是椭圆；
（Ⅱ）设（Ⅰ）中椭圆Γ的左焦点为F，过F点的直线l交椭圆于A，B两点，C为线段AB的中点，当三角形CFO（O为坐标原点）的面积最大时，求直线l的方程．

Answer 1

分析 （Ⅰ）设M的坐标为（x，y），P的坐标为（x_P，y_P），由已知可得$\left\{\begin{array}{l}{{x}_{P}=x}\\{{y}_{P}=\frac{a}{b}y}\end{array}\right.$，由此能求出C的方程；
（Ⅱ）由椭圆C可得c=$\sqrt{{a}^{2}-{b}^{2}}$，左焦点F的坐标．由题意只考虑直线l的斜率存在且不为0即可．设直线l的方程为my=x+1，A（x₁，y₁），B（x₂，y₂），与椭圆的方程联立可得根与系数的关系，再利用中点坐标公式可得y_P，利用S_△CFO=$\frac{1}{2}$|OF|•|y_C|和基本不等式即可得出．

解答 （Ⅰ）证明：设M的坐标为（x，y），P的坐标为（x_p，y_p），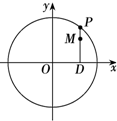
由已知$\overrightarrow{MD}=\frac{b}{a}\overrightarrow{PD}$（a＞b＞0），
可得$\left\{\begin{array}{l}{{x}_{P}=x}\\{{y}_{P}=\frac{a}{b}y}\end{array}\right.$                       
∵P在圆上，
∴x²+（$\frac{ay}{b}$）²=a²，
即C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1．
（Ⅱ）解：由椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1．
∴左焦点F（-c，0）．
由题意只考虑直线l的斜率存在且不为0即可，
设直线l的方程为my=x+c，A（x₁，y₁），B（x₂，y₂），
联立椭圆方程化为（a²+b²m²）y²-2b²cmy-a²b²=0，
∴y₁+y₂=$\frac{2{b}^{2}cm}{{a}^{2}+{b}^{2}{m}^{2}}$，
∴y_C=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{{b}^{2}cm}{{a}^{2}+{b}^{2}{m}^{2}}$，
∴S_△CFO=$\frac{1}{2}$|OF|•|y_C|=$\frac{|{b}^{2}{c}^{2}m|}{2（{a}^{2}+{b}^{2}{m}^{2}）}$
=$\frac{{b}^{2}{c}^{2}}{2（\frac{{a}^{2}}{|m|}+{b}^{2}|m|）}$≤$\frac{{b}^{2}{c}^{2}}{2×2\sqrt{{a}^{2}{b}^{2}}}$=$\frac{b{c}^{2}}{4a}$，
当且仅当|m|=$\frac{a}{b}$时取等号．
此时△CFO的最大值为$\frac{b{c}^{2}}{4a}$，
直线l的方程为±$\frac{a}{b}$y=x+$\sqrt{{a}^{2}-{b}^{2}}$，即为
bx+ay+b$\sqrt{{a}^{2}-{b}^{2}}$=0或bx-ay+b$\sqrt{{a}^{2}-{b}^{2}}$=0．

点评 本题考查点的轨迹方程的求法，直线与椭圆相交问题、根与系数的关系、三角形的面积最大值问题、基本不等式等基础知识与基本技能方法，属于中档题．