
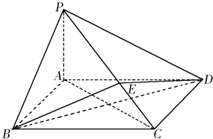
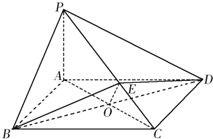
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.| 1 |
| 3 |
| 2 |
| 2 |
| PA2+AC2 |
12+(2
|
| OE |
| PA |
| CE |
| AC |
| OC |
| PC |
| OE |
| 1 |
| CE | ||
2
|
| ||
| 3 |
| ||
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 3 |
| 4 |
| 3 |
| 2 |
| 8 |
| 27 |


科目:高中数学 来源: 题型:
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
查看答案和解析>>
科目:高中数学 来源: 题型:
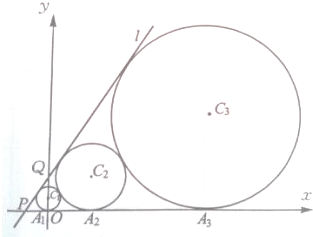 如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,
如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 运输工具 | 途中速度 (千米/时) |
途中费用 (元/千米) |
装卸费用(元) | 装卸时间 (小时) |
运输装卸损耗费用(元/小时) |
| 飞机 | 200 | 15 | 1000 | 2 | 200 |
| 火车 | 100 | 4 | 2000 | 4 | 200 |
| 汽车 | 50 | 8 | 700 | 3 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
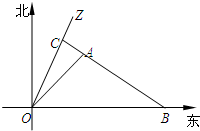 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3| 13 |
| 1 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax |
| x+2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n+1 |
| n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
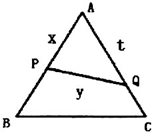 已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求:
已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com