
| ax |
| x+2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n+1 |
| n+1 |
| 2x |
| x+2 |
| 2x |
| x+2 |
| 1 |
| k |
| 2 |
| 2k+1 |
| 1 |
| 1+x |
| 2a |
| (x+2)2 |
| x2+(4-2a)x+(4-2a) |
| (x+1)(x+2)2 |
| a2-2a |
| a2-2a |
| a2-2a |
| a2-2a |
| a2-2a |
| 2x |
| x+2 |
| 2x |
| x+2 |
| 1 |
| k |
2•
| ||
|
| 1 |
| k |
| 2 |
| 2k+1 |
| n |
 |
| k=1 |
| 2 |
| 2k+1 |
| n |
 |
| k=1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n+1 |
| n+1 |


科目:高中数学 来源: 题型:
| sinx |
A、[-
| ||||
B、[
| ||||
C、[2kπ,
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
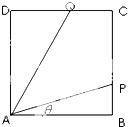 经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=
经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
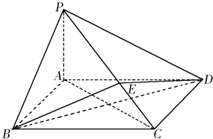 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:
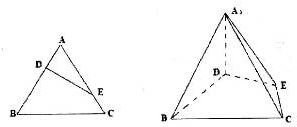 已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足
已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 40 |
| kx+5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com