
分析 根据条件分别求出命题p,q为真命题的等价条件,结合复合命题真假关系建立不等式关系进行求解即可.
解答 解:若p为真,则由f(x)=m+2x为定义在[-1,1]上的“局部奇函数”,
则f(-x)+f(x)=0有解,即2m+2x+2-x=0,
则-2m=2x+2-x,
设t=2x,则t∈[$\frac{1}{2}$,2],
则g(t)=t+$\frac{1}{t}$,在[$\frac{1}{2}$,1]上递减,在[1,2],上递增,
则g(t)∈[2,$\frac{5}{2}$],
则-2m∈[2,$\frac{5}{2}$],得-$\frac{5}{4}$≤m≤-1,
若q为真,则判别式△=(5m+1)2-4>0,
得m>$\frac{1}{5}$或m<$-\frac{3}{5}$,
若“p∧q”为假命题,“p∨q”为真命题,
则p,q一个为真命题一个为假命题,
若p真q假,则$\left\{{\begin{array}{l}{-\frac{5}{4}≤m≤-1}\\{-\frac{3}{5}≤m≤\frac{1}{5}}\end{array}}\right.$,得无交集
若p假q真,则$\left\{{\begin{array}{l}{m>-1或m<-\frac{5}{4}}\\{m>\frac{1}{5}或m<-\frac{3}{5}}\end{array}}\right.$,得$m<-\frac{5}{4}$或$-1<m<-\frac{3}{5}$或$m>\frac{1}{5}$
综上知m的取值范围为$m<-\frac{5}{4}$或$-1<m<-\frac{3}{5}$或$m>\frac{1}{5}$.
点评 本题主要考查复合命题真假关系的应用,根据条件求出命题为真命题的等价条件是解决本题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=2+|x+1| | B. | f(x)=2-x | C. | f(x)=3-|x+1| | D. | f(x)=2x+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲单位 | 87 | 88 | 91 | 91 | 93 |
| 乙单位 | 85 | 89 | 91 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-1,1) | C. | $(-\sqrt{3},-1)$ | D. | $(1,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥b,a∥α,则b∥α | B. | 若α⊥β,a∥α,则a⊥β | C. | 若α⊥β,a⊥β,则a∥α | D. | 若α∥β,m⊥α,则m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
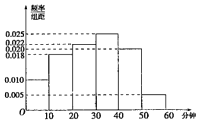 电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:| 非体育迷 | 体育迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com