
| A. | (0,1) | B. | (-1,1) | C. | $(-\sqrt{3},-1)$ | D. | $(1,\sqrt{3})$ |
分析 令t=3x-x3>0,求得函数的定义域,本题即求函数t在定义域内的增区间.再利用导数研究函数的单调性,从而得出结论.
解答 解:令t=3x-x3>0,求得函数的定义域为{x|x<-$\sqrt{3}$,或 0<x<$\sqrt{3}$},且y=lnt,
即求函数t在定义域内的增区间.∵t′=3-3x2,令t′=0,求得x=±1,
由t′的符号可得t的减区间为(-∞,-1)、(1,+∞);增区间为(-1,1).
再结合函数的定义域可得函数t在定义域内的增区间为(0,1),
故选:A
点评 本题主要考查复合函数的单调性,二次函数的性质,利用导数研究函数的单调性,体现了转化的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
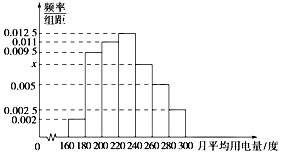 节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 培养液处理 | 未处理 | 合计 | |
| 青花病 | 30 | 224 | 254 |
| 无青花病 | 24 | 1355 | 1379 |
| 合计 | 54 | 1579 | 1633 |
| P(K2≥k) | 0.05 | 0.01 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
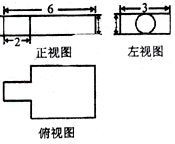 中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )
中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )| A. | 14 | B. | 12+$\frac{π}{2}$ | C. | 12+π | D. | 38+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com