
| 甲单位 | 87 | 88 | 91 | 91 | 93 |
| 乙单位 | 85 | 89 | 91 | 92 | 93 |
分析 (1)先求出甲、乙两个单位职工的考试成立的平均数,以及它们的方差,则方差小的更稳定.
(2)从乙单位抽取两名职工的分数,所有基本事件用列举法求得共10种情况,抽取的两名职工的分数差值至少是4的事件用列举法求得共有5个,由古典概型公式求得抽取的两名职工的分数之差的绝对值至少是4的概率.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{5}$(87+88+91+91+93)=90,$\overline{{x}_{乙}}$=$\frac{1}{5}$(85+89+91+92+93)=90…(2分)
${{s}_{甲}}^{2}$=$\frac{1}{5}$[(87-90)2+(88-90)2+(91-90)2+(91-90)2+(93-90)2]=$\frac{24}{5}$,
${{s}_{乙}}^{2}$=$\frac{1}{5}$[(85-90)2+(89-90)2+(91-90)2+(92-90)2+(93-90)2]=8…(4分)
∵$\frac{24}{5}$<8,∴甲单位职工对法律知识的掌握更为稳定…(5分)
(2)设抽取的2名职工的成绩只差的绝对值至少是4分为事件A,
所有基本事件有:(85,89),(85,91),(85,92)(85,93),(89,85),
(89,91),(89,92),(89,93),(91,85),(91,89),(91,92),
(91,93),(92,85),(92,89),(92,91)(92,93),(93,85),
(93,89),(93,91),(93,92),共20个…(8分)
事件A包含的基本事件有:
(85,89),(85,91),(85,92),(85,93),(89,85),(89,93),
(91,85),(92,85),(93,85),(93,89),共10个…(10分)
∴P(A)=0.5…(12分)
点评 本题主要考查平均数和方差的定义与求法,用列举法计算可以列举出基本事件和满足条件的事件,古典概率的计算公式.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
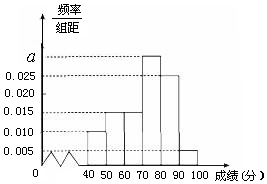 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
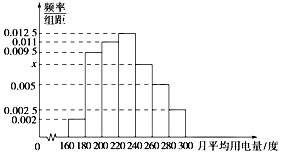 节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com