
| A. | 1 | B. | e | C. | $\frac{1}{e}$ | D. | 0 |
分析 求出${f}^{'}(x)=\frac{a}{x}+1$,${f}^{'}(a)=\frac{a}{a}+1=2$,f(a)=alna+a,由此导数的几何意义求出曲线f(x)在x=a处的切线方程为y-alna-a=2(x-a),再由曲线f(x)=alnx+x在x=a处的切线过原点,能求出a.
解答 解:∵f(x)=alnx+x,∴${f}^{'}(x)=\frac{a}{x}+1$,
∴${f}^{'}(a)=\frac{a}{a}+1=2$,
∵f(a)=alna+a,
∴曲线f(x)在x=a处的切线方程为y-alna-a=2(x-a),
∵曲线f(x)=alnx+x在x=a处的切线过原点,
∴-alna-a=-2a,解得a=e.
故选:B.
点评 本题考查实数值的求法,具体涉及到导数、切线方程、导数的几何意义等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
| 4 | 7 | a1,3 | … | a1,j |
| 7 | 12 | a2,3 | … | a2,j |
| a | a3,2 | a3,3 | … | a3,j |
| … | … | … | … | … |
| ai,1 | ai,2 | ai,3 | … | ai,j |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
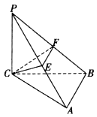 如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.
如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com