
【题目】已知函数![]() .
.
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() ,且对于函数
,且对于函数![]() 的图象上两点
的图象上两点![]() ,
,![]()
![]() ,存在
,存在![]() ,使得函数
,使得函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() .求证;
.求证;![]() .
.
【答案】(1)见解析(2)见证明
【解析】
(1)对函数![]() 求导,分别讨论
求导,分别讨论![]() ,
,![]() 以及
以及![]() ,即可得出结果;
,即可得出结果;
(2)根据题意,由导数几何意义得到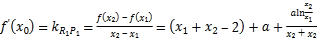 ,将证明
,将证明![]() 转化为证明
转化为证明![]() 即可,再令
即可,再令![]() ,设
,设![]()
![]() ,用导数方法判断出
,用导数方法判断出![]() 的单调性,进而可得出结论成立.
的单调性,进而可得出结论成立.
(1)解:易得,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
①当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.
②当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 或
或![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,
,![]() .
.
③当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
此时,![]() 的减区间为
的减区间为![]() .
.
综上,当![]() 时,
时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() :
:
当![]() 时,
时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.![]() ;
;
当![]() 时,
时,![]() 增区间为
增区间为![]() .
.
(2)证明:由题意及导数的几何意义,得![]()
![]()
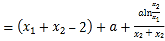
由(1)中![]() 得
得![]() .
.
易知,导函数![]()
![]() 在
在![]() 上为增函数,
上为增函数,
所以,要证![]() ,只要证
,只要证![]() ,
,
即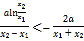 ,即证
,即证![]() .
.
因为![]() ,不妨令
,不妨令![]() ,则
,则![]()
![]() .
.
所以![]()
![]() ,
,
所以![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
即![]() .
.
故有![]() (得证).
(得证).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求二面角![]() 的平面角的正弦值;
的平面角的正弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为10元,被随机分配为1元,2.5元,3元,3.5元,共4份,供甲、乙等4人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于6元的概率是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com