
分析 由圆心在直线y=-4x上,可设圆心C为(a,-4a),圆与直线x+y-1=0相切于点P(3,-2),利用过圆心和P的直线与x+y-1=0垂直,求出a,两点之间的距离公式PC=r,可得圆的标准方程.
解答 解:∵圆心在直线y=-4x上,
设圆心C为(a,-4a),圆与直线x+y-1=0相切于点P(3,-2),
则kPC=$\frac{4a-2}{3-a}$=1,
∴a=1.
即圆心为(1,-4).
r=|CP|=$\sqrt{(3-1)^{2}+(-4+2)^{2}}$=2$\sqrt{2}$,
∴圆的标准方程为(x-1)2+(y+4)=8.
故答案为:(x-1)2+(y+4)=8.
点评 此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,以及直线的点斜式方程,当直线与圆相切时,圆心到切线的距离等于圆的半径.属于基础题.


科目:高中数学 来源: 题型:选择题

| A. | S=19+20;T=19×20 | B. | S=19×20;T=19+20 | ||
| C. | S=1×2×3×…×20; T=1+2+3+…+20 | D. | S=1+2+3+…+20; T=1×2×3×…×20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
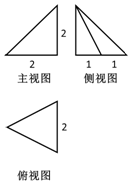
| A. | $\frac{4}{3}$ | B. | $7+\sqrt{5}$ | C. | $5+\sqrt{5}$ | D. | $7+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
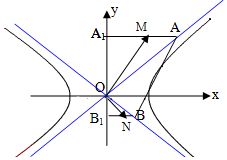 如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )
如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )| A. | $({1,\frac{3}{2}}]$ | B. | $[\frac{3}{2},+∞)$ | C. | $(1,\frac{{\sqrt{5}}}{2}]$ | D. | $[\frac{{\sqrt{5}}}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S△PBC2=S△PAB2+S△PAC2 | B. | S△ABC2=S△PAB2+S△PAC2 | ||
| C. | S△ABC2=S△PAB2+S△PAC2+S△PBC2 | D. | S△PBC2=S△PAB2+S△PAC2+S△ABC2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com