
(本小题满分16分)
心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用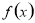 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: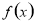
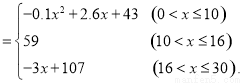
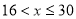
(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
(1)开讲后第5min,符合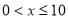 ,求出
,求出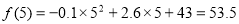 ,开讲后第20min,符合
,开讲后第20min,符合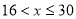 ,求出
,求出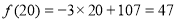 ,相比之下,开讲后第5min学生的接受能力更强一些. (2) 由于
,相比之下,开讲后第5min学生的接受能力更强一些. (2) 由于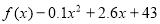 =
=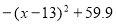 在
在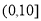 上为增函数,当
上为增函数,当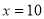 时,
时,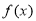 取得最大值
取得最大值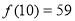 ,当
,当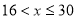 时,
时,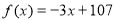 ,当
,当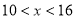 ,
,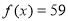 ,在
,在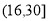 上是减函数,
上是减函数, ,开讲后10min(包括10分钟)学生的接受能力最强,能维持6 min.. (3)一个新数学概念需要55以上(包括55)的接受能力,当
,开讲后10min(包括10分钟)学生的接受能力最强,能维持6 min.. (3)一个新数学概念需要55以上(包括55)的接受能力,当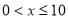 时,
时,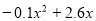
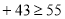 ,解得
,解得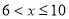 ;当
;当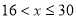 时,
时,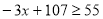 ,解得:
,解得: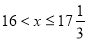 ,持续时间为:
,持续时间为: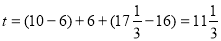 ,不足13min,老师不能在学生一直达到所需接受能力的状态下讲授完这个概念.
,不足13min,老师不能在学生一直达到所需接受能力的状态下讲授完这个概念.
【解析】
试题分析:第一步已知自变量值求函数值,比较后给出答案;第二步是二次函数求最值问题;第三步
试题解析:(1)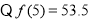 ,
,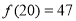 ,则
,则 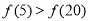
 开讲后第5min比开讲后第20min,学生的接受能力更强一些. ]
开讲后第5min比开讲后第20min,学生的接受能力更强一些. ]
(2)当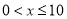 时,
时,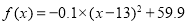
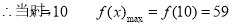 , 当
, 当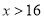 时,
时,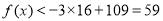
 开讲后10min(包括10分钟)学生的接受能力最强,能维持6 min.
开讲后10min(包括10分钟)学生的接受能力最强,能维持6 min.
(3)由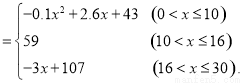
当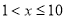 时,
时,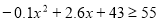 ,得
,得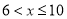 ;
;
当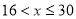 时,
时,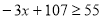 ,得
,得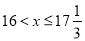
持续时间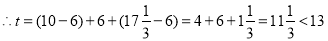
答:老师不能在学生一直达到所需接受能力的状态下讲授完这个概念.
考点:1.求函数值;2.配方法求二次函数的最值;3.分段函数解不等式.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:2014-2015学年山东省枣庄市高三1月月考理科数学试卷(解析版) 题型:选择题
下列说法中正确的是 ( )
A.若命题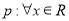 有
有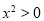 ,则
,则 有
有 ;
;
B.若命题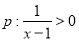 ,则
,则 ;
;
C.若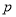 是
是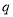 的充分不必要条件,则
的充分不必要条件,则 是
是 的必要不充分条件;
的必要不充分条件;
D.方程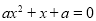 有唯一解的充要条件是
有唯一解的充要条件是
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省等学校高一上学期期中考试数学试卷(解析版) 题型:选择题
函数y=log2 x的反函数和y=log2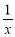 的反函数的图象关于
的反函数的图象关于
A.x轴对称 B.y轴对称 C.y=x对称 D.原点对称
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
设函数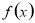 的定义域为
的定义域为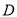 ,若函数
,若函数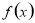 满足条件:存在
满足条件:存在 ,使
,使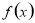 在
在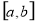 上的值域是
上的值域是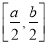 则称
则称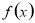 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则的范围是( )
为“倍缩函数”,则的范围是( )
A.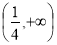 B.
B.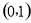
 D.
D. 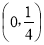
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com