
分析 将不等式左边通分后,利用平方差公式,同角三角函数基本关系式,二倍角的正弦函数公式化简后可得$\frac{8}{si{n}^{2}2α}$+1,利用正弦函数的图象和性质即可得解.
解答 证明:($\frac{1}{si{n}^{4}α}$-1)($\frac{1}{co{s}^{4}α}$-1)
=$\frac{1-si{n}^{4}α}{si{n}^{4}α}$×$\frac{1-co{s}^{4}α}{co{s}^{4}α}$
=$\frac{(1-si{n}^{2}α)(1+si{n}^{2}α)(1-co{s}^{2}α)(1+co{s}^{2}α)}{si{n}^{4}αco{s}^{4}α}$
=$\frac{(1+si{n}^{2}α)(1+co{s}^{2}α)}{si{n}^{2}αco{s}^{2}α}$
=$\frac{2+si{n}^{2}αco{s}^{2}α}{si{n}^{2}αco{s}^{2}α}$
=$\frac{2}{si{n}^{2}αco{s}^{2}α}$+1
=$\frac{8}{si{n}^{2}2α}$+1≥9.
点评 本题主要考查了平方差公式,同角三角函数基本关系式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了正弦函数的图象和性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
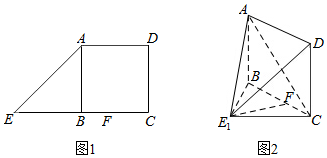 如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.
如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | 2或-1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
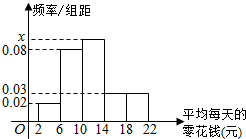 为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )
为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )| A. | 780 | B. | 680 | C. | 648 | D. | 460 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B. | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | ||
| C. | |$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | 以上答案都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com