
分析 利用椭圆、双曲线的定义,结合余弦定理,证明PF1⊥PF2,即可求出△PF1F2的外接圆半径.
解答 解:由题意,|PF1|+|PF2|=2$\sqrt{10}$,|PF1|-|PF2|=2$\sqrt{8}$,
∴|PF1|=$\sqrt{10}$+2$\sqrt{2}$,|PF2|=$\sqrt{10}$-2$\sqrt{2}$,
∵|F1F2|=6,
∴cos∠F1PF2=$\frac{20+16-36}{2(10-8)}$=0,
∴PF1⊥PF2,
∴△PF1F2的外接圆半径为3.
故答案为:3.
点评 本题考查椭圆、双曲线的定义,考查余弦定理,考查学生的计算能力,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
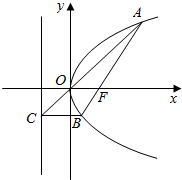 过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.
过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{59}{117}$ | D. | $\frac{11}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com