
已知函数
(1)求函数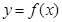 的单调区间;
的单调区间;
(2)若函数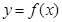 的图像与直线
的图像与直线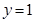 恰有两个交点,求
恰有两个交点,求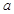 的取值范围.
的取值范围.
(1)递增区间为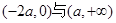 ,递减区间为
,递减区间为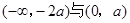 (2)
(2)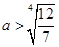 或
或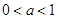 .
.
解析试题分析:(1)利用导数求函数单调区间,关键明确定义域,正确求出导函数. 因为
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区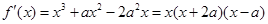 ,令
,令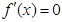 得
得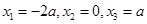 由
由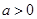 时,列表分析
时,列表分析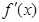 在
在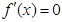 根的左右的符号,得
根的左右的符号,得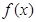 的递增区间为
的递增区间为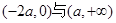 ,
,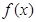 的递减区间为
的递减区间为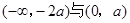 ,(2)由(1)得到
,(2)由(1)得到 ,
,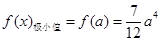
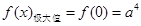 ,要使
,要使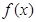 的图像与直线
的图像与直线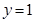 恰有两个交点,只要
恰有两个交点,只要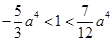 或
或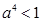 ,即
,即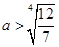 或
或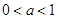 .
.
解:(1)因为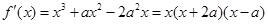 2分
2分
令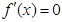 得
得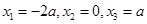
由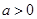 时,
时,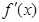 在
在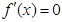 根的左右的符号如下表所示
根的左右的符号如下表所示
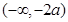
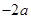
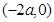
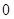
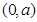
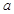
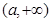
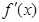
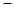
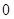
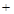
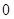
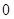


聚焦小考冲刺48天系列答案
聚焦新中考系列答案
鸿翔教育决胜中考系列答案
绝对名师系列答案
开心教程系列答案
开心15天精彩寒假巧计划江苏凤凰科学技术出版社系列答案
考出好成绩系列答案
考能大提升系列答案
考前一搏系列答案
考易通初中全程复习导航系列答案
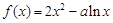 .
.
(1)若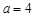 ,求函数
,求函数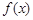 的极小值;
的极小值;
(2)设函数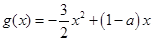 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量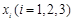 使得
使得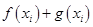 的值相等,若存在,请求出
的值相等,若存在,请求出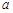 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由? 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.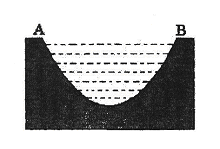
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号