Question

20．设f（x）是定义在R上的奇函数，且对任意x∈R，都有f（x+2）=-f（x），当0≤x≤1时，f（x）=x²．
（I）当-2≤x≤0时，求f（x）的解析式；
（II）设向量$\overrightarrow a=（2sinθ，1），\overrightarrow b=（9，16cosθ）$，若$\overrightarrow a，\overrightarrow b$同向，求$f（\frac{2017}{sinθ+cosθ}）$的值；
（III）定义：一个函数在某区间上的最大值减去最小值的差称为此函数在此区间上的“界高”．
求f（x）在区间[t，t+1]（-2≤t≤0）上的“界高”h（t）的解析式；在上述区间变化的过程中，“界高”h（t）的某个值h₀共出现了四次，求h₀的取值范围．

Answer 1

分析 （I）定义在R上的奇函数，可得f（-x）=-f（x），f（x+2）=-f（x），当0≤x≤1时，f（x）=x²．可求当-2≤x≤0时，求f（x）的解析式
（II）根据$\overrightarrow a，\overrightarrow b$同向，建立关系，利用向量的乘积的运算法则化简即可求解．
（III）根据题意，证明其对称性，根据函数解析式画出图形，数形结合法，可求h₀的取值范围．

解答 解：（ I）设-2≤x≤-1，则0≤x+2≤1，
∴f（x+2）=（x+2）²=-f（x），
∴f（x）=-（x+2）²；
设-1≤x≤0，则0≤-x≤1，
∴f（-x）=（-x）²=-f（x），
∴f（x）=-x²．
综上：当-2≤x≤0时，$f（x）=\left\{{\begin{array}{l}{-{{（x+2）}^2}，（-2≤x≤-1）}\\{-{x^2}，（-1≤x≤0）}\end{array}}\right.$．
（ II）由题：$32sinθcosθ=9⇒sinθcosθ=\frac{9}{32}$，∴${（sinθ+cosθ）^2}=1+2sinθcosθ=\frac{25}{16}$，
所以$sinθ+cosθ=±\frac{5}{4}$．∵sinθcosθ＞0，∴θ可能在一、三象限，
若θ在三象限，则$\overrightarrow a，\overrightarrow b$反向，与题意矛盾；若θ在一象限，则$\overrightarrow a，\overrightarrow b$同向．综上，θ只能在一象限．
∴$sinθ+cosθ=\frac{5}{4}$，∴$f（\frac{2017}{sinθ+cosθ}）=f（2017×\frac{4}{5}）=f（2015×\frac{4}{5}+2×\frac{4}{5}）=f（403×4+\frac{8}{5}）$，（※）
由f（x+2）=-f（x）得f（x+4）=-f（x+2）=-[-f（x）]=f（x），
所以（※）式=$f（\frac{8}{5}）=-f（\frac{8}{5}-2）=-f（-\frac{2}{5}）=f（\frac{2}{5}）={（\frac{2}{5}）^2}=\frac{4}{25}$（或0.16）
（ III）先说明对称性（以下方法均可）：
法一：由（ II）：f（x+4）=f（x），再由已知：f（x）是奇函数且f（x+2）=-f（x），得f（x-2）=-f（x）=f（-x），令x为-x，得f（-2-x）=f（x），
∴f（x）的图象关x=-1对称．
法二：由（ I）：x∈[-1，0]时，f（-2-x）=-（-2-x）²=-（x+2）²=f（x）；x∈[-2，-1]时，f（-2-x）=-（-2-x+2）²=-x²=f（x），
综上：f（x）在[-1，0]和[-2，-1]上的图象关于x=-1对称．
法三：由画出图象说明f（x）在[-2，-1]和[-1，0]上的图象关于x=-1对称也可．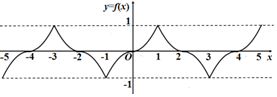

设f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），则h（t）=M（t）-m（t）．显然：区间[t，t+1]的中点为$t+\frac{1}{2}$．所以，如图：
（ i）当t≥-2且$t+\frac{1}{2}≤-1$，即$-2≤t≤-\frac{3}{2}$时，M（t）=-（t+2）²，m（t）=-1，∴h（t）=M（t）-m（t）=-（t+2）²+1；
（ ii）当t+1≤0且$t+\frac{1}{2}≥-1$，即$-\frac{3}{2}≤t≤-1$时，M（t）=-（t+1）²，m（t）=-1，∴h（t）=M（t）-m（t）=-（t+1）²+1；
（ iii）当-1≤t≤0时，M（t）=（t+1）²，m（t）=-t²，∴h（t）=M（t）-m（t）=（t+1）²+t²=2t²+2t+1．
综上：$h（t）=\left\{{\begin{array}{l}{-{{（t+2）}^2}+1，（-2≤t≤-\frac{3}{2}）}\\ \begin{array}{l}-{（t+1）^2}+1，（-\frac{3}{2}≤t≤-1）\\ 2{t^2}+2t+1，（-1≤t≤0）\end{array}\end{array}}\right.$．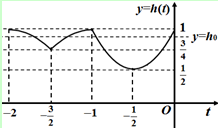
根据解析式分段画出图象，并求出每段最值（如图），由图象可得：$\frac{3}{4}＜{h_0}＜1$．

点评 本题考查了函数解析式的求法，分段函数最值讨论，新定义的理解，周期，对称性的判断，属于综合题．难度大．