
���� ��I��������ɵã�2a=2$\sqrt{2}$��a+c=$\sqrt{2}$+1������a2=b2+c2������������ɵó���
��II������ֱ��l�ķ���Ϊ��y=k��x-1����A��x1��y1����B��x2��y2����ֱ�߷�������Բ����������Ϊ����1+2k2��x2-4k2x+2k2-2=0�����ø���ϵ���Ĺ�ϵ���е����깫ʽ�ɵ��߶�AB���е�G$��\frac{2{k}^{2}}{1+2{k}^{2}}��\frac{-k}{1+2{k}^{2}}��$��
��k=0ʱ����������k��0ʱ������|MA|=|MB|����kMG•k=-1����Ϊ2k2-3k+1=0�����k��
�ڵ�x��x��ʱ��ֱ��l�ķ���Ϊx=1��������Բ���̽��y=$��\frac{\sqrt{2}}{2}$���ɵ�S��ABO=$\frac{\sqrt{2}}{2}$����ʱֱ��l�ķ���Ϊ��x=1����k=0ʱ����ABO�����ڣ���ȥ����k��0ʱ���ɵ�S��ABO=$\frac{1}{2}��1��|{y}_{1}-{y}_{2}|$=$\frac{1}{2}|k��{x}_{1}-1��-k��{x}_{2}-1��|$=$\frac{|k|}{2}|{x}_{1}-{x}_{2}|$=$\frac{1}{2}\sqrt{{k}^{2}}$$•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$�����ɵó����ۣ�
��� �⣺��I��������ɵã�2a=2$\sqrt{2}$��a+c=$\sqrt{2}$+1������a2=b2+c2��
���a=$\sqrt{2}$��c=1=b��
����Բ�ķ���Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}$=1��
��II������ֱ��l�ķ���Ϊ��y=k��x-1����A��x1��y1����B��x2��y2����
����$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$��������1+2k2��x2-4k2x+2k2-2=0��
��x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$��x1•x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$��y1+y2=k��x1+x2-2��=$\frac{-2k}{1+2{k}^{2}}$��
���߶�AB���е�G$��\frac{2{k}^{2}}{1+2{k}^{2}}��\frac{-k}{1+2{k}^{2}}��$��
��k=0ʱ����������
k��0ʱ��������|MA|=|MB|��
��kMG•k=$\frac{\frac{-k}{1+2{k}^{2}}-\frac{1}{2}}{\frac{2{k}^{2}}{1+2{k}^{2}}-0}$•k=-1����Ϊ2k2-3k+1=0��
���k=1��$\frac{1}{2}$��
���Ͽɵã�����������k��ֵΪ0��1��$\frac{1}{2}$��
�ڵ�x��x��ʱ��ֱ��l�ķ���Ϊx=1��������Բ���̽��y=$��\frac{\sqrt{2}}{2}$��
�ɵ�S��ABO=$\frac{\sqrt{2}}{2}$����ʱֱ��l�ķ���Ϊ��x=1��
��k=0ʱ����ABO�����ڣ���ȥ��
��k��0ʱ���ɵ�S��ABO=$\frac{1}{2}��1��|{y}_{1}-{y}_{2}|$=$\frac{1}{2}|k��{x}_{1}-1��-k��{x}_{2}-1��|$
=$\frac{|k|}{2}|{x}_{1}-{x}_{2}|$=$\frac{1}{2}\sqrt{{k}^{2}}$$•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$
=$\frac{1}{2}\sqrt{{k}^{2}}$•$\sqrt{��\frac{4{k}^{2}}{1+2{k}^{2}}��^{2}-4��\frac{2{k}^{2}-2}{1+2{k}^{2}}}$=$\frac{\sqrt{2}}{\;}$$\sqrt{2}\sqrt{\frac{{k}^{2}��{k}^{2}+1��}{��1+2{k}^{2}��^{2}}}$=$\frac{\sqrt{2}}{2}$$\sqrt{\frac{{k}^{2}��{k}^{2}+1��}{��{k}^{2}+\frac{1}{2}��^{2}}}$��$\frac{\sqrt{2}}{2}$��
��S��ABO��$\frac{\sqrt{2}}{2}$�����k��0ʱ�������ڷ���������ֱ��l��
�������������ҽ���ֱ��l�ķ���Ϊx=1ʱ��S��ABO�����ֵΪ$\frac{\sqrt{2}}{2}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ���������۷�����������������㹫ʽ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-$\frac{��}{6}$ | B�� | x=$\frac{��}{12}$ | C�� | x=-$\frac{��}{12}$ | D�� | x=$\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{{\sqrt{2}}}{10}$ | B�� | $-\frac{{7\sqrt{2}}}{10}$ | C�� | $-\frac{{3\sqrt{2}}}{4}$ | D�� | $-\frac{{4\sqrt{2}}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AA1��BB1ΪԲ��OO1��ĸ�ߣ�BC�ǵ���ԲO��ֱ����D��E�ֱ���AA1��CB1���е㣬BA=2��AC=1��B1C=3
��ͼ��AA1��BB1ΪԲ��OO1��ĸ�ߣ�BC�ǵ���ԲO��ֱ����D��E�ֱ���AA1��CB1���е㣬BA=2��AC=1��B1C=3�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{4}{3}$ | B�� | -$\frac{3}{4}$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
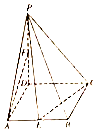 ��ͼ��������P-ABCD�У�����ABCDΪ���Σ���DAB=60�㣬PD��ƽ��ABCD��PD=AD=4����E��F�ֱ�ΪAB��PD���е㣮
��ͼ��������P-ABCD�У�����ABCDΪ���Σ���DAB=60�㣬PD��ƽ��ABCD��PD=AD=4����E��F�ֱ�ΪAB��PD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com