
分析 (1)根据复数的几何意义以及复数的基本运算即可求$\overrightarrow{AD}$对应的复数;
(2)根据复数的几何意义以及复数的基本运算即可$\overrightarrow{DB}$对应的复数;
(3)根据条件求出复数的模长以及根据三角形的面积公式即可△APB的面积.
解答  解析 (1)∵$\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{AB}$=(1,4)-(3,2)=(-2,2),
解析 (1)∵$\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{AB}$=(1,4)-(3,2)=(-2,2),
∴与$\overrightarrow{AD}$对应的复数为-2+2i.
(2)$\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}$=(3,2)-(-2,2)=(5,0),
∴与$\overrightarrow{DB}$对应的复数为5.
(3)由(1)可知|$\overrightarrow{AD}$|=2$\sqrt{2}$,|$\overrightarrow{AB}$|=$\sqrt{13}$,|$\overrightarrow{DB}$|=5,
由余弦定理,求得
cosA=$\frac{8+13-25}{2•2\sqrt{2}•\sqrt{13}}$=$\frac{-4}{4\sqrt{26}}$.
∴cosA=$\frac{-1}{\sqrt{26}}$,∴sinA=$\frac{5}{\sqrt{26}}$.
∴S△ADB=$\frac{1}{2}$•|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•sinA=$\frac{1}{2}$•$\sqrt{13}$•2$\sqrt{2}$•$\frac{5}{\sqrt{26}}$=5.
∴S△ADB$\frac{1}{2}$×5=$\frac{5}{2}$.
点评 本题主要考查复数的基本运算以及复数的几何意义,利用复数的几何意义以及余弦定理求三角形的面积.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=8y | B. | x2=2y | C. | x2=4y | D. | x2=2$\sqrt{2}$y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误导致结论错误 | |
| B. | 小前提错误导致结论错误 | |
| C. | 推理形式错误导致结论错误 | |
| D. | 大前提和小前提都错误导致结论错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
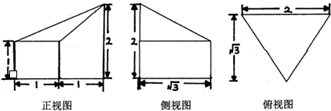
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com