
分析 根据|$\overrightarrow{a}$-t$\overrightarrow{b}$|的最小值得出$\overrightarrow{a},\overrightarrow{b}$的夹角为θ=60°,设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,$\overrightarrow{OM}=2\overrightarrow{a}$,则$\overrightarrow{MC}$=$\overrightarrow{c}-2\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{c}-\overrightarrow{b}$,由($\overrightarrow{c}$-2$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=0得出C在以BM为直径的圆P上,求出圆P的半径和OP的长,从而得出|$\overrightarrow{c}$|的最小值.
解答 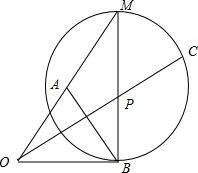 解:设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,
解:设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,
∵|$\overrightarrow{a}-t\overrightarrow{b}$|$≥\frac{\sqrt{3}}{2}$,
∴1+t2-2tcosθ≥$\frac{3}{4}$,即t2-2cosθ•t+$\frac{1}{4}$≥0.
∴△=4cos2θ-1=0,
∴cosθ=$\frac{1}{2}$.即单位向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为60°.
设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,$\overrightarrow{OM}=2\overrightarrow{a}$,
则$\overrightarrow{MC}$=$\overrightarrow{c}-2\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{c}-\overrightarrow{b}$,
∵($\overrightarrow{c}$-2$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=0,∴MC⊥BC.
∴C在以BM为直径的圆P上.
∵OB=OA=1,∠AOB=60°,OM=2,
∴圆P的半径r=BP=$\frac{1}{2}BM$=$\frac{\sqrt{3}}{2}$,OP=$\sqrt{O{B}^{2}+B{P}^{2}}$=$\frac{\sqrt{7}}{2}$.
∴OC的最小值为OP-r=$\frac{\sqrt{7}-\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{7}-\sqrt{3}}}{2}$.
点评 本题考查了平面向量线性运算的几何意义,平面向量的数量积运算,属于中档题.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com