
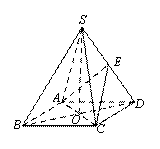
如图,在四棱锥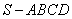 中,底面
中,底面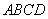 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,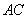 与
与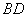 的交点为
的交点为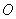 .
.
(1)求证: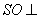 平面
平面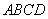 ;
;
(2)已知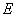 为侧棱
为侧棱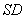 上一个动点. 试问对于
上一个动点. 试问对于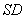 上任意
上任意
一点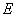 ,平面
,平面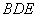 与平面
与平面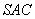 是否垂直?若垂直,请加以
是否垂直?若垂直,请加以
证明;若不垂直,请说明理由.
 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
在边长为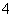 的正方形
的正方形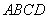 中,
中,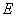 、
、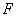 分别为
分别为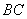 、
、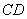 的中点,
的中点,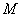 、
、 分别为
分别为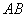 、
、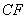 的中点,现沿
的中点,现沿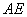 、
、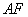 、
、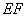 折叠,使
折叠,使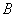 、
、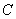 、
、 三点重合,构成一个三棱锥.
三点重合,构成一个三棱锥.
(1)判别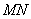 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)证明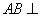 平面
平面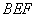 ;
;
 (3)求多面体
(3)求多面体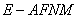 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有
A.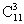 种 B.
种 B.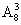 种 C.
种 C.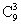 种 D.
种 D.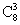 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com