Question

12．点P（x，y）是直线kx+y+3=0上一动点，PA，PB是圆C：x²+y²-4y=0的两条切线，A，B是切点，若四边形PACB面积的最小值为2，则k的值为（　　）

• A． $2\sqrt{2}$
• B． $±2\sqrt{2}$
• C． 2
• D． ±2

Answer 1

分析 由“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”，最后利用点到直线的距离求出直线的斜率即可．

解答 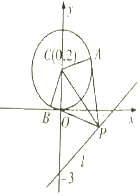解：如图，${S_{PACB}}=2{S_{△PAC}}=|{PA}|•|{AC}|=2|{PA}|=2\sqrt{{{|{PC}|}^2}-{{|{AC}|}^2}}=2\sqrt{{{|{PC}|}^2}-4}$，
∴当|PC|最小时，面积取最小值，而|PC|最小即为点C到直线l的距离d，
又$d=\frac{5}{{\sqrt{{k^2}+1}}}$，
∴$2\sqrt{{d^2}-4}=2⇒{k^2}=4⇒k=±2$．
故选D．

点评 本题的考点是直线与圆的位置关系，主要涉及了构造四边形及其面积的求法，解题的关键是“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”属于中档题．