
已知数列{an}的各项均为正数,前n项和为Sn,且满足2Sn=a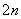 +n-4(n∈N*).
+n-4(n∈N*).
(1)求证:数列{an}为等差数列;
(2)求数列{an}的通项公式.
解:(1)证明:当n=1时,有2a1=a +1-4,
+1-4,
即a -2a1-3=0,
-2a1-3=0,
解得a1=3(a1=-1舍去).
当n≥2时,有2Sn-1=a +n-5,
+n-5,
又2Sn=a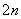 +n-4,
+n-4,
两式相减得2an=a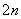 -a
-a +1,
+1,
即a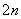 -2an+1=a
-2an+1=a ,也即(an-1)2=a
,也即(an-1)2=a ,
,
因此an-1=an-1或an-1=-an-1.
若an-1=-an-1,则an+an-1=1.
而a1=3,所以a2=-2,这与数列{an}的各项均为正数相矛盾,所以an-1=an-1,
即an-an-1=1,因此数列{an}为首项为3,公差为1的等差数列.
(2)由(1)知a1=3,d=1,
所以数列{an}的通项公式
an=3+(n-1)×1=n+2,即an=n+2.


科目:高中数学 来源: 题型:
如图,一艘船上午9∶30在A处测得灯塔S在它的北偏东30°的方向,之后它继续沿正北方向匀速航行,上午10∶00到达B处,此时又测得灯塔S在它的北偏东75°的方向,且与它相距8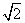 n mile.此船的航速是________n mile/h.
n mile.此船的航速是________n mile/h.
查看答案和解析>>
科目:高中数学 来源: 题型:
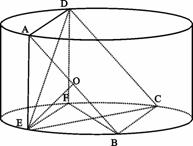
如图所示,圆柱的高为2,底面半径为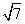 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过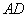 作圆柱的截面交下底面于
作圆柱的截面交下底面于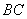 , 四边形ABCD是正方形.
, 四边形ABCD是正方形.
(Ⅰ)求证 ;
;
(Ⅱ)求四棱锥E-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知Sn是等差数列{an}的前n项和,S10>0并且S11=0,若Sn≤Sk对n∈N*恒成立,则正整数k构成的集合为( )
A.{5} B.{6}
C.{5,6} D.{7}
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an},则“an,an+1,an+2(n∈N*)成等比数列”是“a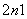 =anan+2”的( )
=anan+2”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,且Sn=4an-3(n∈N*).
(1)证明:数列{an}是等比数列;
(2)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
将石子摆成如图的梯形形状,称数列5,9,14,20,…为梯形数,根据图形的构成,此数列的第2 012项与5的差即a2 012-5=( )
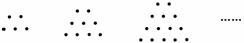
A.2 018×2 012 B.2 018×2 011
C.1 009×2 012 D.1 009×2 011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com