练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    　已知等比数列{an}中，a2＝32，a8＝，an＋1<an.

    (1) 求数列{an}的通项公式；

    (2) 设Tn＝log2a1＋log2a2＋…＋log2an，求Tn的最大值及相应的n值．


    解：(1) ， an＋1<an，所以q＝.以＝64为首项，所以通项公式为an＝64·n－1＝27－n(n∈N)．　

    (2) 设bn＝log2an，则bn＝log227－n＝7－n.所以{bn}是首项为6，公差为－1的等差数列．

    Tn＝6n＋ (－1)＝＝＋.因为n是自然数，所以n＝6或n＝7时，Tn最大，其最大值是T6＝T7＝21.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    以下四个命题：其中真命题为(　　)

    ①从匀速传递的产品生产流水线上，质检员每20分钟从中抽取一件产品进行某项指标检测，

    这样的抽样是分层抽样；

    ②两个随机变量相关性越强，则相关系数的绝对值越接近于1；

    ③在回归直线方程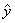＝0.2x＋12中，当解释变量x每增加一个单位时，预报变量平均增加

    0.2个单位；

    ④对分类变量X与Y，它们的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握

    程度越大．

    A．①④        　B．②④            C．①③   　　D．②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等差数列{an}中

    (1) 已知a4＋a14＝2，则S17＝________；

    (2) 已知a11＝10，则S21＝________；

    (3) 已知S11＝55，则a6＝________；

    (4) 已知S8＝100，S16＝392，则S24＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}中，S3＝7，S6＝63，则an＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若数列{an}的前n项和为Sn＝，则数列{an}的通项公式是an＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在数列{an}中，若a1＝1，an＋1＝an＋2(n≥1)，则该数列的通项an＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn为数列{an}的前n项和，已知a1≠0，2an－a1＝S1·Sn，n∈N．

    (1) 求a1，a2，并求数列{an}的通项公式；

    (2) 求数列{nan}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，若∠A＝60°，∠B＝45°，BC＝3，则AC＝________．

    查看答案和解析>>

    同步练习册答案