
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
分析 利用圆心到直线的距离小于半径可得到直线与圆相交,可求出满足条件的k,最后根据几何概型的概率公式可求出所求.
解答 解:圆(x-3)2+y2=1的圆心为(3,0),半径为1.
要使直线y=kx与圆(x-3)2+y2=1相交,
则圆心到直线y=kx的距离$\frac{|3k|}{\sqrt{{k}^{2}+1}}$<1,解得-$\frac{\sqrt{2}}{4}$<k<$\frac{\sqrt{2}}{4}$.
在区间$[-\sqrt{2},\sqrt{2}]$中随机取一个实数k,则事件“直线y=kx与圆(x-2)2+y2=1相交”
发生的概率为$\frac{\frac{\sqrt{2}}{2}}{2\sqrt{2}}$=$\frac{1}{4}$.
故选:B.
点评 本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
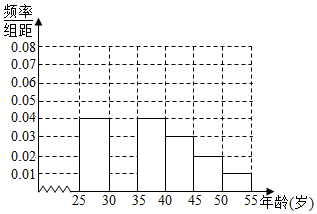
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元)
某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元) 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
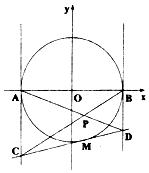 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)在区间$[\frac{3π}{4},π]$上单调递增 | |
| C. | 函数f(x)的图象关于直线$x=-\frac{7π}{12}$对称 | |
| D. | 函数f(x)的图象关于点$(\frac{7π}{12},0)$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com